【文╱洪介興】
●現象1╱10÷6的答案 小數點後會循環
小明是一位小學五年級的學生,他們正學到商數可以是小數的除法,用功的小明如往常一般,自己隨意設定數字,出一些題目來自我練習,起初兩題「41÷25=1.64」和「17÷8=2.125」還算得好好地,想不到第3題就碰上了大問題。
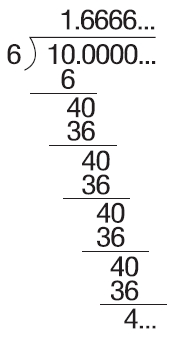
原來他第3題設定的題目是10÷6,計算時會無止盡地重複「商數填6」、「40-36=4」、「補0」的步驟,因此商數是1.6666……,小數點後竟然是無窮無盡的6!
小明嚇壞了,拿著計算紙跑去問姊姊,想不到姊姊沒有露出絲毫驚訝,冷靜地告訴小明:「這個商數叫做『循環小數』,可以記錄成『1.6』,意思就是小數點後面跟著無限多個6。」小明跟著寫下「0.5」並說:「那麼這就是小數點後面跟著無限多個5的意思囉!」
「沒錯!」姊姊接著說:「而且你寫的正是5÷9的計算結果喔!」看姊姊說得如此自信,小明仍不禁懷疑,但動筆一算竟果真如此。
「太神奇了!你怎麼能一眼看出0.5是5÷9的計算結果?」小明完全無法相信。姊姊對小明的訝異置之不理,繼續說:「厲害的還不只如此,你試著算算看『47÷11』和『5÷37』,應該會得到更有趣的結果!」
到底「47÷11」和「5÷37」會得到什麼神奇的結果呢?請讀者們拿出紙筆,和小明一起試著計算看看,自己實際動筆算過更能體會箇中趣味喔!
●算算看╱1÷7到6÷7 有何奧妙在其中?

哇!不得了!」算完47÷11後的小明驚呼著:「這次是4.272727……,小數點後面不斷重複著『27』!」姊姊說:「是的,那麼你猜猜看這個無窮無盡不斷循環著的小數要怎麼記錄呢?」小明思考了一下,寫下「4.27」。
「非常正確!」姊姊高亢的聲調完全傳達了內心的喜悅:「趕快接著算下一個例子,『5÷37』吧!」
經過一小段時間,小明再度驚呼:「天啊!這次是0.135135 ……,『135』不斷地循環耶!我知道了,這次可以寫成這樣對吧?」小明一邊說著,一邊寫下「0.135」。
「正是如此!更有趣的還在後頭,要試試看嗎?」不等小明回答,姊姊馬上接著說:「這次請你一口氣把『1÷7』、『2÷7』、『3÷7』、『4÷7』、『5÷7』、『6÷7』都算過,雖然有點多,但對你而言應該不難吧!」
姊姊話說完還不忘使出激將法,性格被摸透的小明果然中招,馬上低頭猛算,聰明的讀者們也請拿出紙筆試試看吧,可別讓小明專美於前囉!
●現象2╱6個不同的運算 重覆相同的動作
「終於算完了!」小明整理了他的計算結果如圖。
「竟然要算到小數點後第7位才開始循環,而且每個計算結果都是這樣,真酷!」小明讚歎道。
「才不只這樣呢!回想一下,你不覺得雖然這看起來是6個不同的運算,你卻一直重複做著相同的動作嗎?」
「嗯……1的後面是4,4的後面是2,2的後面是8……真的耶!每一題都是按照『1→4→2→8→5→7』的順序在循環,只是開頭的數字不同而已,太神奇了吧!」
會有這樣的結果,是因為當除以7的運算做到只剩一位數的時候,若非整除就是餘1、餘2、餘3、餘4、餘5、餘6這6種情形。
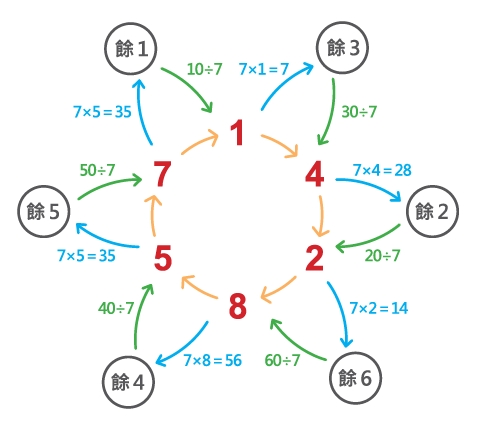
如果看到餘1,還要繼續除下去的話,下一位商數必定是1,且下一個餘數是3;如果看到餘3,下一位商數必定是4,且下一個餘數是2;如果看到餘2,下一位商數必定是2,且下一個餘數是6;如果看到餘6,下一位商數必定是8,且下一個餘數是4;如果看到餘4,下一位商數必定是5,且下一個餘數是5;如果看到餘5,下一位商數必定是7,且下一個餘數是1。至此,餘數轉了一圈又回到餘1,商數當然也會一起隨之循環;由前討論可知,不論從哪一個餘數開始,接續的餘數、商數都會遵守相同的固定順序。
●再試試╱2÷17到16÷17 從計算中看答案
「這真是太有趣了!還有更多這樣的例子嗎?」小明等不及想多看一些類似的案例。「是嗎?那也得看你有沒有這個本事囉!」不知不覺,姊姊似乎已經把小明牽著鼻子走。
姊姊繼續說:「下一個挑戰是『1÷17』,可別中途放棄囉!」小明說:「才一題而已,看我兩三下把它解決!」報紙前的讀者也請接下這份挑戰書吧!
經過一番努力,小明終於算出來了,「1÷17」的計算結果竟是0.0588235294117647,直到算完小數第16位才出現重複的餘數,因此商數從小數第17位才開始循環!

「下一個挑戰是求出『2÷17』、『3÷17』、『4÷17』……一直到『16÷17』的答案。」不給小明喘息,姊姊又發起下一個挑戰。小明連忙道:「這怎麼可能算得完……」
不等小明繼續抱怨,姊姊搶著解釋:「是要你『求』出來,可不是要你『算』出來,再說得更確切些,你要試著從剛才的計算過程中『看』出來。試試看吧,我很看好你喔!」不負姊姊的期望,小明不久便「看」出了全部的答案。
●問問你╱除以17 小數第17位起循環 若除27 小數第27位才循環?
「除以7的時候從小數第7位開始循環,除以17的時候從小數第17位開始循環,那麼除以27的時候就是從小數第27位開始循環囉?」小明提出了他的猜想。
「這是個很好的猜想,可惜不是這樣。」姊姊解釋道:「7和17是質數,而27是合數,用它們當除數所形成的循環小數位數,沒辦法直接合在一起討論喔!」
小明接著說:「那麼除以任意質數p的時候就是從小數第p位開始循環,這次總對了吧?」姊姊回答:「照你這樣說,除以11的時候就是從小數第11位開始循環囉?但剛才除以11的時候是從小數第3位就開始循環的耶!」小明迷惑道:「啊!那到底是怎樣呢?」
「聽好囉!」姊姊回答道:「用任意的質數p當除數,到小數第p位一定會循環。」小明快弄糊塗了:「這不就是我剛才的意思嗎?」
「不一樣喔!」姊姊解釋道:「『寫到小數第p位一定會循環』意思就是到小數第p位時,有可能已經循環不只一次了!再換句話說,到小數第p-1位的時候,一定會剛好完成循環,但完成的循環次數則不一定!」
姊姊繼續解釋:「譬如用11當除數時,2位數就是一循環,到小數第10位已完成5次循環;用13當除數時,6位數就是一循環(如右圖),到小數第12位時已完成2次循環;而用17當除數時,到小數第16位只完成1次循環。」

小明已經聽得眼花撩亂,但富有科學精神的他,還是說出了最重要的那三個字:「好吧,原來是這樣,這又是『為什麼』呢?」
「問得好!假設p是除了2或5以外的任意質數,只要連續寫p-1個9,就一定是p的倍數,譬如99是3的倍數,999999(6個9)是7的倍數,999999999999(12個9)是13的倍數」
小明驚訝道:「那麼連續寫22個9也會是23的倍數囉?」
「沒錯!至於『為什麼』連續寫p-1個9,就一定是p的倍數;以及『為什麼』這個性質跟循環小數有關呢?我要趕著出門,改天再繼續玩下去吧!」
【2023-05-15/聯合報/R07版/好讀周報動腦力】

-300x181.jpg)