文╱洪介興
●問題1╱3個數相加為12 請問有幾種組合
你的思考有條理嗎?首先請你挑戰看看這個問題:
挑選3個不同的正整數,使它們的總和是12,請問總共有幾種不同的組合?
如3+7+2和7+2+3這般只是調換相加順序的,算是同一種組合,請先試著想過再繼續看下去喔。
公布答案:總共有7種組合,分別是:
1+2+9、1+3+8、1+4+7、1+5+6,和2+3+7、2+4+6,以及3+4+5。
觀察力敏銳的讀者可能會發現,上面這7個算式的陳列是有其邏輯的。因為如果只是隨意地抓數字來湊,很容易就會有重複或遺漏,所以要有系統地進行思考才能又快速又正確,這裡所採用的思考邏輯如下:
①因為調換相加順序算同一種組合,所以算式中的數一律由小而大排列。
②先固定最小的數是1,找出有使用到1的所有組合後,再把最小的數換成2,然後再換成3。
③最小的數固定下來時,中間的數由小而大一個一個列舉,譬如最小的數固定是1時,中間的數先放2,再放3、4、5。
在有系統的列舉下,我們可以很肯定這就是所有的可能性,沒有重複、也沒有遺漏,這就是系統性思考的威力。
●問題2╱連接5圈不重複 請問有幾種路線
瞭解了系統性思考的精神後,再請你接著挑戰下面這個問題:
下圖中有5個小圈圈,其中有一些線段將它們相連,挑選其中一個小圈圈出發,用一筆畫把每個小圈圈都恰好走過一遍,走過的地方(包括起點)都不能重複,請問共有幾種不同的路線?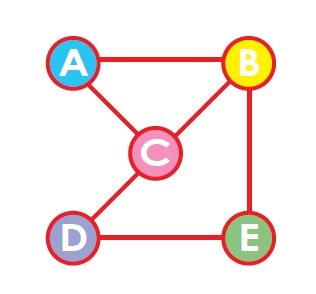
譬如A→C→D→E→B就算是一種走法,但C→A→B→C→D→E則不行,因為C重複了。這裡還是要提醒你,先嘗試過後再繼續看下去喔!
公布答案:總共有14種不同路線,分別是:
1. A→B→C→D→E
2. A→B→E→D→C
3. A→C→B→E→D
4. A→C→D→E→B
5. B→A→C→D→E
6. B→E→D→C→A
7. C→A→B→E→D
8. C→D→E→B→A
9. D→C→A→B→E
10. D→E→B→A→C
11. D→E→B→C→A
12. E→B→A→C→D
13. E→D→C→A→B
14. E→D→C→B→A
從以上的排列,可以看出這是有系統地逐點仔細搜索結果,不會有遺漏,也不會有重複。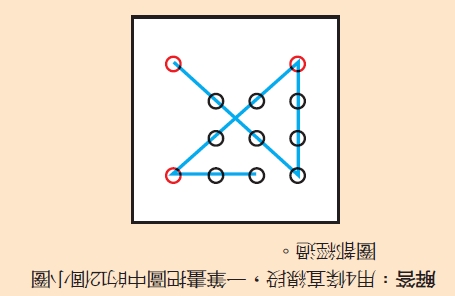
●問題3╱如何用4條直線 一筆連起9圈
接著再來挑戰下面這個問題:
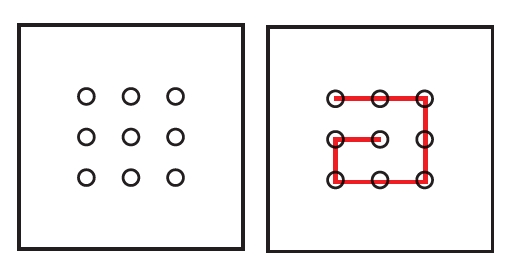
圖中有9個小圈圈,請用4條直線段,一筆畫把9個小圈圈都經過。
旁邊是一個失敗的例子,因為它用到了5條直線段。
請仔細思考後再繼續往下讀。
如果你經過系統性思考後,發現這是一道不可能做出來的題目,表示你的思考相當縝密喔!
●問題4╱如何用4條直線 一筆連起12圈
接著我們看下一道很類似的題目:
請用4條直線段,一筆畫把圖中的12個小圈圈都經過。
完成這一題後,再回頭看看前面那道要畫9個點的題目,只要把這一題多出來的3個點視而不見,就和前一道題目一模一樣了,這時候你有沒有突然恍然大悟,原來前一道題是可以解出來的!
我們之所以會解不出9個點的題目,其實是因為被自己的思考框架所侷限,由於沒想到可以畫到超出9個圈圈的範圍,才會一直完成不了!因此我們要突破思考的框架,但這要怎麼辦到呢?
突破思考的框架,聽起來好像是靠創意,但其實還是要建立在邏輯的基礎上。以前面9個點的題目為例子,要經過縝密的系統性思考後,才能確定在原本的規則下沒有解決辦法,進而才能意識到,一定要放寬某些規則才有機會解開這個問題。
●問題5╱改用3條直線 能否連起9圈
緊接而來的下一個挑戰是:
請用3條直線段,一筆畫把前面圖中的9個小圈圈都經過!
你能夠辦到嗎?可不要急著投降喔!
題目給的雖然是9個小圈圈,但我們很容易把它們侷限成9個「點」,而忽略了其實可以利用圈圈有一個範圍的這個特性。
用一條直線段把同一橫排的3個圈圈串在一起時,其實可以不必用水平線,而是可以用微微傾斜的直線段,現在請你想像一個寫得非常、非常、非常寬的「Z」字,它就是這一題的答案囉!你有沒有想到呢?
原本我們以為一筆畫的4條直線段辦不到的題目,不但完成得了,現在竟然還能用一筆畫的3條直線段完成,是不是很驚奇、很有趣呢?
●問題6╱只用一條直線 能否穿過9圈
下一個挑戰更會讓你大吃一驚:
請用一條直線段把圖中的9個小圈圈都經過!
你能通過這個終極挑戰嗎?有個方法是把紙張捧到眼睛的高度,從紙張的側面看過去,這時候9個小圈圈是不是都落在同一條直線上了呢?
上面這個答案雖然很有創意,但恐怕有些人會覺得這個解法過於牽強,那麼也請參考下面這個解法,看看是否更具有說服力。
首先畫三條貫穿整張紙的水平線,每條線各經過3個同一橫排的小圈圈,接著把紙張捲起來,讓剛才畫好的水平線兩端得以碰觸,但要以下圖的方式錯開一行,如此一來,3條直線段就變成同一條線了!不過,這條彎掉的直線還算不算得上是一條直線呢?這可能就見仁見智囉!
●終極題╱62-63=1 如何讓算式成立
今天的最後一個問題來了:
62-63=1
只移動一個數字,使上面的算式變成正確的。
把減號前面的6或2移到減號後或等號後都不可能,因為這樣減法做起來會變成負數;把減號後面的6或3移到減號前或等號後也不可能,把1移到等號左邊更不可能;因此,只有單純的減法是無法解開這道題的,勢必要突破框架。
想到了嗎?答案就是把6拿到2的右上角,變成2的6次方,也就是64,這麼一來,算式2的6次方-63=1就正確了!
縝密的系統性思考,除了能讓我們毫無遺漏地進行搜索,甚至還能讓我們在排除所有可能性後,意識到必須放寬規則、跳脫框架,才能探索更多的可能性!也就是說,創造力並非天馬行空,而往往建立在縝密的思考之上。
●作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中
原文出自《好讀周報》665期

-300x200.webp)
