文╱洪介興
●等速加法╱1分鐘增加9 2分鐘顯示多少?
請你想像一台機器,我們姑且稱它是等速加法機器吧。這台機器有一個顯示數字的螢幕,會顯示當前的數值,最初的起始值是0;一個旋鈕,可以調整螢幕上的數值每分鐘要增加多少;按下開始鍵後,螢幕上的數值會根據你設定的速度增加;按下暫停鍵,螢幕上的數值就會暫停變化;最後還有一個重設鍵,按下後,螢幕上的數值會恢復到0。特別要補充的是,螢幕上的數值並非等到1分鐘到了才突然增加,而是隨時做連續的變化。
舉例來說,螢幕上一開始顯示的數值是0,如果把加法速度設定為每分鐘增加9,按下開始鍵、1分鐘後按暫停,此時螢幕上的數值會是9。那麼請問你,如果是2分鐘後才按下暫停鍵,螢幕上的數值會是多少?另外,如果半分鐘後就按暫停,螢幕上的數值又該是多少?
每分鐘增加9,多1分鐘就是再加9,所以若是2分鐘後才按暫停,螢幕上的數值會是18;至於半分鐘,應該是增加9的一半,若是半分鐘就暫停,數值應該是4.5。
●等速乘法╱1分鐘變9倍 半分鐘顯示多少?
另一台機器,姑且稱它是等速乘法機器。它的構造和等速加法機器一樣,有一個顯示當前數值的螢幕、一個旋鈕、開始鍵、暫停鍵和一個重設鍵。不同之處在於,旋鈕所控制的是螢幕上的數值每分鐘要變為幾倍,而非每分鐘增加多少;另外,螢幕上的起始數值是1,而不是0,因為乘法對0發揮不了作用,0是加法世界的起點,而1是乘法世界的起點。
接著來看一個等速乘法機器運作的例子,螢幕上原本顯示著1,如果我們把乘法速度設定為每分鐘9倍,在按下開始鍵的1分鐘後按暫停,螢幕上就會是9。問題來了,如果是2分鐘後才按暫停鍵,螢幕上的數值是多少?如果半分鐘後就按暫停,螢幕上的數值又該是多少?
每分鐘變為9倍,多1分鐘就是再變為9倍,所以若是2分鐘後才按暫停,螢幕上的數值顯然會是81,如果再多1分鐘,那就是再9倍,變成729;但如果半分鐘就按暫停呢?
●看答案╱變化倍率要相同 半分鐘會顯示3
一個很直覺的想法:從1開始變化,1分鐘後會變成9,所以半分鐘應該會在1和9的正中間,也就是5。上面的想法雖然不無道理,但其實這是加法的思維,不適用此處。
另一個可能的想法:既然1分鐘後會變成9倍,那麼半分鐘應該就是9的一半,4.5倍,而1的4.5倍就是4.5。這個想法看似更合理,但深入思考會發現,前半分鐘從1變成4.5,這樣是4.5倍;而後半分鐘從4.5變成9,這樣是2倍,兩者倍率不同。既然機器是做「等速乘法」,照理前半分鐘、後半分鐘的變化倍率應該要相同才對吧!
討論到此,答案應該呼之欲出了。因為前半分鐘的變化倍率,要和後半分鐘的變化倍率相同,而且經過兩次乘法要變為9倍,9=3×3,所以,在半分鐘按下暫停時,螢幕上應該是3才對。
依循這個道理,如果把乘的速度調到每分鐘25倍,因為25=5×5,所以半分鐘就是變5倍;當乘倍的速度調成每分鐘100倍時,100=10×10,所以半分鐘就是10倍。
●考考你╱每分鐘變2倍 半分鐘顯示多少?
現在我們應該相當熟悉等速乘法機器的運作了,最後的挑戰來了:如果把乘倍的速度調到每分鐘2倍,半分鐘就按暫停,這時候螢幕上的數值會是多少呢?
聰明的你應該已經想到,就是要找一個自己乘以自己剛好等於2的數囉!1.4×1.4是1.96,太小;1.5×1.5是2.25,又太大,那到底是多少呢?
如果螢幕上的數值可以顯示3位小數,那麼半分鐘後,螢幕上會是1.414,把這個數自己乘以自己會得到1.999396,雖然已經非常接近2,但仍不是2。事實上,再多位小數,都沒辦法寫出一個自己乘以自己剛好等於2的數,甚至用分數也辦不到!原因有點複雜,但我試著用簡單的方式來說明。
如果拿一個小數自己乘以自己,絕不可能小數點後全為0,就像1.414自己乘以自己,算出的小數最後一位是6,所以絕對寫不出一個自乘會等於2的小數。至於分數,任何最簡分數自乘以後,得出的答案一定無法進行任何約分,所以也就不可能有一個分數自乘以後可以約分成2。
●想想看╱小數分數寫不出來 自己乘自己怎表達
小數寫不出來,分數也寫不出來,會不會是這個數本來就不存在呢?
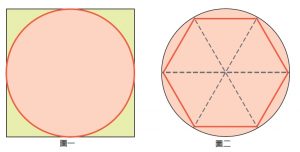
不,這個數當然存在,他就存在於正方形的對角線上!如圖三所示,假設每個小正方形的邊長是1,面積也是1,四個小正方形的對角線,圍出了一個轉45度角的正方形,不難看出這個正方形的面積是2,但邊長是多少呢?沒錯,就是它!自己乘以自已要等於2,大約1.414,用小數或分數都無法完整表達的那個數!
我們知道有些數用小數無法表達,只能用分數表達,現在又冒出一個連分數也無法表達的數,這時候便需要一個新的記錄方法,因此我們用「 √2 」來表示這個自己乘以自己會等於2的數,它讀作「根號2」;同理,√3 、√5 、√6 就表示自己乘以自己會等於3、等於5、等於6的那些數,大約是1.732、2.236、2.449。
●告訴你╱紙張尺寸 暗藏√2特性
進行文書作業時,最常見的紙張尺寸大概不外乎A3、A4、B4、B5,而這些紙張尺寸中其實暗藏著很厲害的特性。把A3的紙從長邊對半切,就會變成兩張A4;而把B4從長邊對半切,就會變成兩張B5。厲害的是,當我們把切完的紙張轉90度後,你會覺得紙張跟原來相比只是縮小了,沒有變得比較胖或比較瘦。事實上,你還可以繼續把A4對切成A5,把A5對切成A6;也可以反過來把兩張A3合併成A2,兩張A2合併成A1,紙張形狀都不會改變。
我們會感覺形狀不變,是因為紙張的長邊和短邊比值固定;你是否納悶,怎麼根號講到一半,突然另闢主題呢?這是因為若想讓紙張對切後形狀不變,則長邊和短邊的比值就必須符合自己乘以自己等於2,也就是 !(圖四)
以我們非常熟悉的A4紙張為例,它的長邊是297公釐、短邊是210公釐,比值約為1.41429,而 的近似值為1.41421,之間的誤差不到萬分之一。可見A4規格的發明人非常有數學素養呢!
●作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中並指導政大橋藝社
原文出自《好讀周報》620期