文╱洪介興
●考考你╱檢測準確率99.9% 為何確診率10%?
22013年底,日本NHK頻道上映一部名為《數學女孩的戀愛事件簿》連續劇。在第二集中,男主角從準確率高達99.9%的檢測中,得知自己罹患了大約每10000人才會有1個人得到,罕見的不治之症,他只能把希望寄託在檢測結果有誤,然而檢測發生錯誤的機率只有千分之一,看來用九死一生都不足以描述男主角的絕境,而是九九九死一生啊!
但頭腦冷靜的女主角從男主角口中得知此事後,卻告訴男主角,說他患病的機率不是99.9%,而是只有10%才對!這到底是怎麼一回事呢?
女主角之所以有這樣的結論,簡而言之,是因為檢測錯誤的機率雖然很低,然而相較於一個人得病的機率卻高上許多;千分之一縱使罕見,但相較於萬分之一就不是那麼稀罕了。
女主角在劇中如此說明:
檢查的正確率是99.9%,也就是10000人來檢查,會給9990個人正確的結果,剩下0.1%的10個人則是錯誤的結果。真正患病的只有10000人中的1個人,然而被檢查為患病的卻有10個人左右,因此你患病的機率不是99.9%,而是10人中的1人,只是10%的問題。
一個數學嗅覺敏銳的觀眾看了這個片段,可能會發現女主角的說明其實未盡詳細,而且數據也大幅簡化了,事實上,男主角患有該疾病的機率約為9.08%,如圖一所示。-e1618220224466.jpg)
依照女主角的說明方式,若有10000人接受檢驗,無患病但錯被驗出陽性的人數期望值應該是9.999人,而有患病且正確被驗出陽性的人數期望值應該是0.999人,即便粗略的用10人和1人來計算,男主角有患病機率也應該是11分之1(約為9.09%),而非10分之1,然而考量到戲劇的流暢性,這樣的犧牲是可以理解的。
●告訴你╱什麼情況去檢驗? 不同前提影響機率
上述的數據瑕疵還只是小問題,更讓人在意的其實是一個未被劇情交待的大問題:「男主角為何會去做這個檢驗呢?」這個重要的資訊甚至可能會翻轉女主角原本的結論!
假想以下的狀況:如果男主角是因為身體出現某些症狀而就醫,醫師根據過往的紀錄,知道有這些症狀的人當中,大約每20人中就有1人是罹患了那個不治之症,因而安排男主角進行檢驗。若是上述前提,那麼在檢測結果出來前,男主角患有該病症的機率就不像一般人是萬分之一,而是20分之1。這個機率比檢驗錯誤的可能性高出數十倍。
如圖二所示,我們可計算出在此狀況下,當檢驗結果為陽性時,患有該病的機率約為98.13%,雖不至於像男主角一開始誤以為的99.9%這麼糟,但也已經是希望渺茫。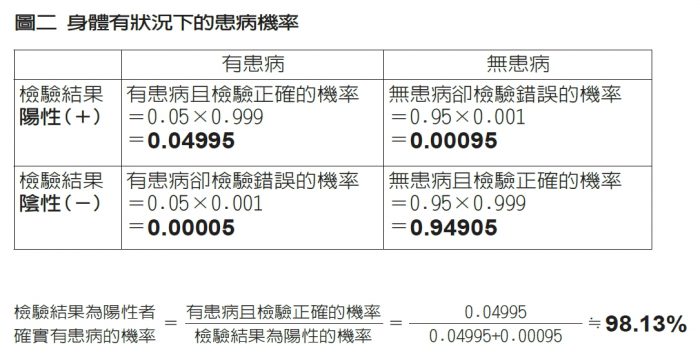
●要注意╱盛行率影響精密性 擴大檢驗效益有限
以上所論,當一個人被檢驗為陽性,而他實際上當真有患病的機率,被稱為該檢驗的「精密性」。由前面的討論我們可以知道,精密性不光是取決於檢驗本身的準確率,還受到「疾病盛行率」所影響,盛行率指的是受檢驗群體患有該疾病的比例。當盛行率極低時,即便檢驗本身的準確率很高,推算出的精密性還是會很低;反之盛行率越高,反映出的精密性才會跟著比較高。劇中案例便是如此,當盛行率只有萬分之一時,檢驗的精密性不到10%,但當盛行率為20分之1時,精密性則超過98%。
去年11月底,我國駐美外交領事館的59人,全員進行新冠肺炎的快篩檢測,其中9名檢驗出陽性,舉國譁然;但在經過更準確的PCR檢驗後,證實是虛驚一場,9名人員都是偽陽性。會發生這樁烏龍事件主要有兩個原因,其一是快篩的準確率原本就比較低,容易發生偽陽性的情形;其二是台灣的防疫成效極佳,即便是在風險相對較高的駐外領事館,疾病盛行率仍然極低,由前面的討論可知,在極低的疾病盛行率下,檢驗的精密性也會很低。
有了前面的討論基礎,不難了解為什麼新冠肺炎的疫情爆發至今一年多來,許多國家都做過規模較大的檢驗,但台灣一直沒有跟進。因為以台灣的疾病盛行率來看,可預見大規模檢驗的實質效益必然極低,且大量的偽陽性還會帶來更多的後續處理問題,造成人力和物資的不必要浪費。面對這場長期抗戰,我們還是應該把寶貴的防疫能量用在最迫切的地方。公共議題不能只憑感覺,而是要有科學性的討論,這才是現代公民所應具備的素養。
●想想看
世界都開始進行疫苗施打。然而疫苗的防護率並不是100%,也就是說,有些人即便接種了疫苗,仍有受到感染的可能;另外,有些人的身體狀況根本不適合進行接種。這麼說來,新冠肺炎的疫情是否永遠不會有終止的一天呢?其實不然,因為事實上,要達到群體免疫,並不需要所有人都具備免疫力。
要說清楚這個問題,我們得從「基本傳染數」(R0值)開始談起。R0值是一名患者平均會傳染出去的人數,流行病學專家多研判新冠肺炎的R0值大約在3附近。意即假若一開始只有1名患者,我們且稱他為第一代患者;他在病癒前大約會傳染3個人,且稱為第二代患者;這3名第二代患者大約會傳染給9名第三代患者;然後大約有27名第四代患者……,以此類推。
R0值只由病毒特性和社會原本的運作模式所決定,而在考量防疫措施後,每一名患者平均會傳染出去的人數一定會比原本的R0值還低,這個新的數字稱為「有效傳染數」(Rt),若Rt大於1,表示新患者比前一代的患者還多,則疫情將越來越嚴重;而若Rt可以一直維持在小於1,表示新患者會一直比前一代的患者還少,則疫情將有宣告終結的一天,因此Rt維持小於1就稱為群體免疫,那麼我們的下一個問題就是,要怎麼運用疫苗把Rt降到小於1呢?
我們現在假設有100名剛得新冠肺炎的患者,以R0值是3來計算,他們原本應該會傳染給3倍的人數,也就是300名新患者;但如果這300人當中有超過200人具有免疫力,那麼實際被傳染的新患者就只有不到100人,比上一代的患者還少。從這個例子我們可以了解,如果R0值是3,當3分之2以上的人具有免疫力時,新一代的患者就會比前一代還少;而如果R0值是4,則需要4分之3以上的人具有免疫力,才可達到群體免疫。
看到這裡,是否覺得人類戰勝病毒、一切回歸平常已近在眼前呢?但在那一天到來之前,我們每個人對各項防疫措施可不能鬆懈喔!
●作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中並指導政大橋藝社
原文出自《好讀周報》612期