Blog

【文╱洪介興】

●二元一次能解題 一元一次也能解

今天讓我們先來做一道像是數學課本或習作裡會見到的題目：

提示①：父、子兩人歲數的總和是46歲。

提示②：父親歲數的2倍加上兒子歲數的3倍，正好是100歲。

問題：父、子兩人的年齡各是幾歲？

在繼續閱讀下去之前，請先想想看，你會怎麼做這道題目呢？

題目中清楚地寫明了兩個數量關係，並且都包含兩個未知的量：父親的歲數和兒子的歲數。因此，一個很自然的想法就是列出二元一次聯立方程式，接著用代入消去法或加減消去法求出x和y的值，圖一是運用代入消去法解題的過程。

如果把上面這道問題，拿去問還沒學過二元一次方程式，但學過一元一次方程式的同學，雖然他只能假設一個未知數，但還是可以解這道問題，做法如圖二。

你是否有發現，兩種解法其實非常相像呢？

二元一次方程式的解法，是將兩個未知的量都假設成未知數，把兩個數量關係各列成一條方程式，進而求出兩個未知數的值；而在一元一次方程式的解法中，只把其中一個未知的量假設成未知數x，然後運用了提示①，把另一個未知的量用含有x的算式來表達，接下來就可以用提示②列出完整的方程式。

眼尖的你可能還會發現，在二元一次的解法中，「將y=46-x代入(2)式」後所得到的方程式，就跟一元一次的解法中所列出的方程式一模一樣。也就是在這道題目中，一元一次方程式的解法，其實可以看作是暗地裡用了代入消去法的二元一次方程式解法。

●只用四則運算 圖形也可以解題

如果拿這道題目去問沒有學過方程式的學生，他能不能解開這道題目呢？

善用圖解常能幫助我們解決許多問題，圖中的綠色條代表父親的年齡，橘色條代表兒子的年齡，所以全部5條的總和是100。

同時，我們又知道1個綠色條、1個橘色條的總和是46，因此圖中的兩個紅框圈起來的部分都是46，那麼剩下1個沒被圈到的橘色條就是 100-46×2=8，因此1個綠色條就是46-8=38。

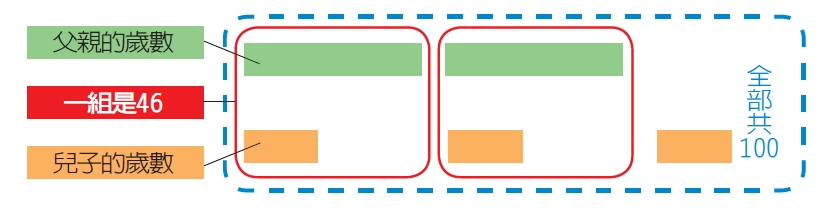
不知道你有沒有發現，上面這個圖解的做法，就如同用加減消去法，將2x+3y=100和2x+2y=92的左、右兩邊分別相減，得到y=8是一樣的呢！

●較複雜的題目 二元一次輕鬆解

既然二元一次方程式的題目，用一元一次方程式，甚至不用方程式也能解決，那我們為什麼還要學到二元一次方程式呢？讓我們來看下面這道問題：

每顆水梨的價格相等、每顆蘋果的價格也相等，且

提示①：3顆水梨比4顆蘋果還貴5元

提示②：7顆水梨和5顆蘋果總共800元

問題：每顆水梨和蘋果的價格各是幾元？

這題如果運用二元一次方程式的方法，假設兩個未知數，可以很輕易地列出符合題意的兩道方程式，剩下的工作就是單純的計算，也完全難不倒我們。根據這個問題列出的二元一次聯立方程式如圖四。

●同樣一道題目 一元一次較吃力

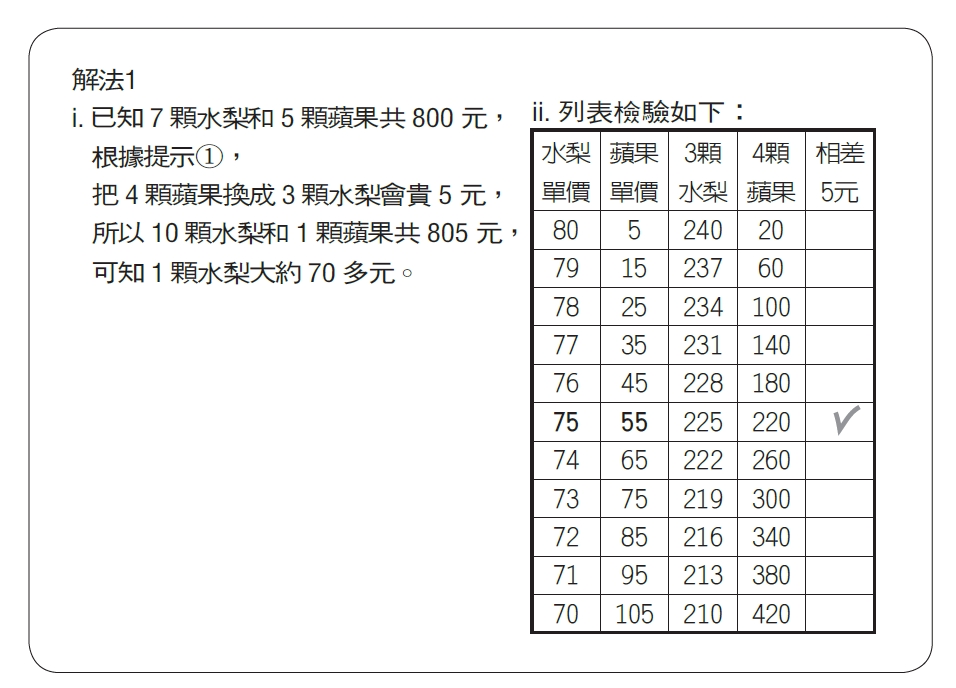
如果不用兩個未知數，而是只假設一個未知數，要列出正確的一元一次方程式就不太容易了。以下提供兩個解法，都是先假設每個水梨x元，差別在於解法1是運用提示①把蘋果的價錢用含有x的算式來表達，然後根據提示②來列方程式；而解法2是相反過來，運用提示②把蘋果的價錢用含有x的算式來表達，然後根據提示①來列方程式。兩個解法的複雜程度不相上下，都要經過許多步驟的仔細思考才能列出方程式，從假設未知數到列出方程式為止的解題過程如圖五。

●都不用方程式 算數方法也能解

如果都不用方程式呢？那麼事情就會變得相當有趣，這邊提供兩個解法，在繼續閱讀下去之前，邀請你也試著不用方程式來解這道題目。

●設定合適未知數 代數解題無堅不摧

前面這兩種不使用方程式，只靠運算來進行解題的方式叫做算數方法，運用方程式進行解題的方式叫做代數方法。

代數方法的威力在於，只要設定合適的未知數，往往可以輕易地依照情境列出正確的關係式，最後只需要求出方程式的解。許多算數方法很難解的問題，用代數方法都能輕易地迎刃而解，任何題目在代數方法面前都是一視同仁的──設未知數、列方程式、求解，代數方法就像是一台穩定、高效的解題機器，代數方法的美，是一種規律的美。

相反地，算數方法在比較複雜的題目經常碰壁，會需要從中觀察、分析出題目的要害，甚至可能需要一些特殊的操作讓題目變得好解決。然而，正因為如此，算數方法常會展現出思維的美妙，每道題目都有不同的漂亮解法，甚至同一道題目就有好多不同的精彩解法，算數方法的美，是一種創造的美。

你是代數方法的信徒，還是算數方法的信徒呢？若想要成為數學達人，我誠心地建議你，兩者都不要偏廢，要貪心地把魚與熊掌都兼得，每一道題目端到我們面前，都要反覆思量，尋找更多不同的美妙解法，享受解題的樂趣，感受數學的美！

●作者為教育部適性教學計畫「數學建築活動」教案設計人，任教北市石牌國中

【2023-03-20/聯合報/R07版/好讀周報動腦力】