第一次段考成績出爐,拿到理化考卷,還滿意嗎? 升國二的同學,理化是首次出現的課程。 升國三的學長姐們,已被理化折磨了一年,成了難以駕馭的科目。 要把理化學好,有幾個重點必須掌握。以下歸納了幾個招式來和大家分享,他山之石,可以攻錯。
【文╱林志鴻】
●作者為高雄小港國中自然科老師,喜歡在課堂上穿插各種小故事,啟發孩子對科學的興趣。
●招式1╱以不變應萬變 找出什麼不會變
先對首次學習理化的同學來說明:
理化基本上是兩個科目:物理和化學。
在國中兩個科目合成一個科目,到了高中以後就會分成兩個科目。
基礎科學有數學、物理、化學和生物。
數學,是科學的工具,自成一個科目。
生物,主要是研究生命的科學,在國一已經學習完畢;國三再出現的生物會比國一的課程更進階。
物理,主要是學習物體本身在時空具有的性質、運動狀態、各種能量間的變化關係。簡單來說,就是物質的道理。
化學,主要是學習物質在產生變化時和其他物質之間的關係。簡單來說,就是變化的學問。
物理和化學就是學習非生命部分的科學,學習物質在時間和空間的變化。在變化的過程中,我們會特別強調「不變的因素」是什麼,這個「不變的因素」就是方程式的「等號」。變化前放在等號的左邊,變化後放在等號的右邊,如此就能解出我們需要的未知數。
基本上,支撐理化這幢房子的兩根柱子是物質和能量,分別是:質量守恆定律和能量守恆定律。守恆的原意是指遵守不變的原理,所以遇到守恆定律就要特別留意。
●招式2╱化抽象為具體 融入生活經驗
再來是專業術語的定義與練習。專業術語是進入專業領域和同儕溝通的基本能力,在科學領域裡一定不能混淆含糊的就是基本定義。
國二進入理化課程,遇到的第一個關卡是密度,我就用密度來說明。
密度的定義:單位體積內所含物質的多寡。
這樣的文字內容,好像在背國文的注釋,很難了解具體的意義,轉換一下說明。
單位體積的意思,就像是同樣教室的空間,每間教室的空間都要一樣大。
我們把物質當作同學們,所以:
「單位體積內所含的物質」的意思可以轉換為
「一間教室裡有多少同學」,這叫做人口的稠密程度。
教室裡的人愈多,就愈擁擠,代表密度愈大。
水的密度是1g/cm3;鐵的密度是7.8g/cm3。可以想像
水是一間教室裡有1個人;而鐵是一間教室裡有7.8個人。
要把密度的定義轉換成自己能理解的性質,這樣才會有感覺,才能進行複雜的推理,才會有能力去判斷這個推理合不合理。
例如:
質量相同下,體積愈小的,密度愈大。
可以想像成
人數相同下,教室愈小,人和人之間就愈擁擠,所以密度要愈大。
這種將定義轉換成日常生活相似的對應,是很重要的能力養成。
●招式3╱符號、意義、單位 了解公式3特質
定義之後就會有式子,還是以密度為例:
D=M╱V
公式會以符號的形式出現,所以每條式子都有符號、意義和單位三項特質。
我們會運用符號來進行運算,單位是測量時所使用的標準,理化很重視單位。
密度的單位是g/cm的3次方,念法是每立方公分含有多少公克的物質;分母的單位先念,要加上「每」這個字,再念分子的單位。
水的密度是1g/cm的3次方,念作每立方公分含1公克的水;
鐵的密度是7.8g/cm的3次方,念作每立方公分含7.8公克的鐵。
會念單位,就能了解在運算過程中的變化。
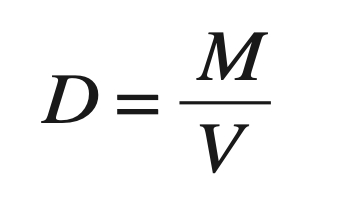
●招式4╱建立解釋圖表 理解圖表意涵
接著就是要理解圖表的意涵。還是以密度為例:
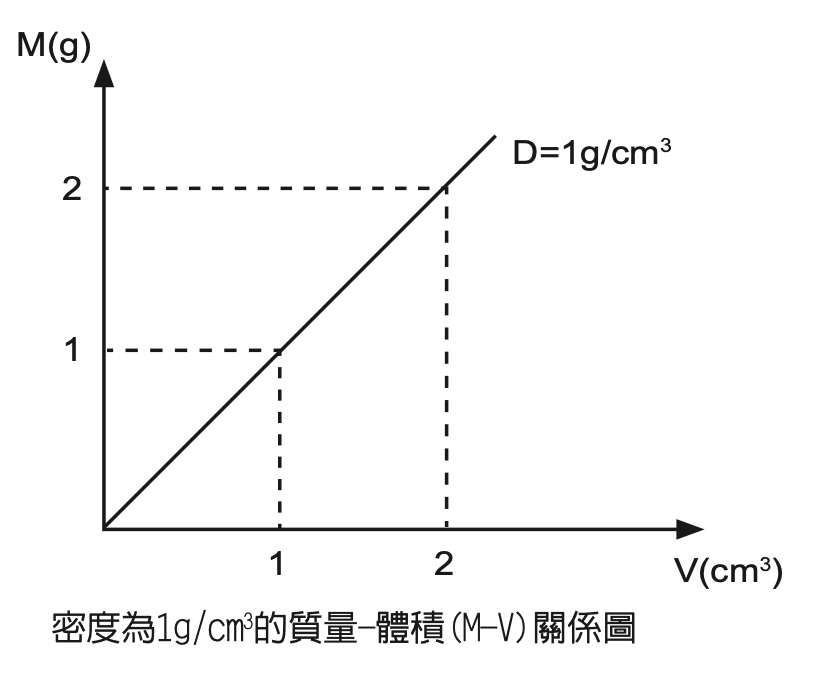
先思考密度為(1g/cm的3次方)的質量-體積(M-V)關係圖:
若V=1cm的3次方,則M=1g;
V=2cm的3次方,則M=2g……
依此類推,可以畫出通過原點的斜直線,如圖二。
接著畫出密度為(2g/cm的3次方)的質量-體積(M-V)關係圖:
若V=1cm的3次方,則M=2g;
V=2cm的3次方,則M=4g……,
依此類推,可以畫出通過原點的紅色斜直線,畫在相同的圖上,如圖三。
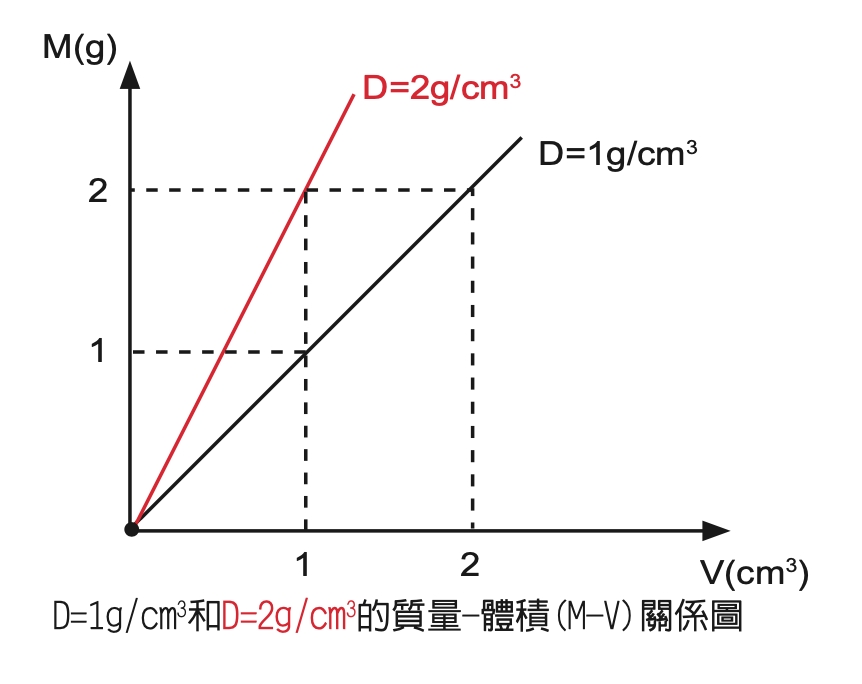
由此可以得出結論:
斜直線愈靠近M軸的密度愈大。
在整個理化課程中,牽涉到的定義大致只有三個符號,所以把密度的學習基礎立穩了,往後的課程都會遇到相似的推論方式,一直重複相似的技巧。只要熟能生巧,就可以把理化學得很不錯。
●招式5╱好的解題習慣 容易查錯訂正
沒有例外,解題是檢驗觀念及鍛鍊技巧的不二法門。
理化的題目都是應用題,大多是從日常生活中遇到的問題而衍生出來的。好的解題習慣可以讓自己找出觀念錯誤的地方,也容易在做錯時找到應該訂正的地方,所以準備一張計算紙是很重要的,將計算過程寫下來。很多同學都沿襲小學的習慣,在計算紙上只作數字的運算。但計算不是只有數字的運算而已,記住!要把公式的符號寫出來,必須養成利用符號運算的習慣(這對將來高中課程非常有用),最後再將數字代進去,解出正確的答案。還是用密度來說明,如圖四。
●招式6╱勤解題累積實力 抓重點看懂題目
我常勉勵同學們,一定要親自作功課,實力才是自己的。有那麼多的題目,怎麼可能做得完?但能稱得上「經典範例」的就那麼幾題,千變萬化的題目大部分都是從那些經典範例裡演變出來的。
再反過來想想,解完這些題目的實力會成為會考的得分機會,更積極一點,培養這些實力是為了讓自己在高中遇到相同等級的高手,將來在求學過程中可以互相勉勵、砥礪、扶持及成長,豈不樂哉?
光看同學來問的方式就可以分出高下:
①指著問題說:老師,這題要怎麼算?(這是跨出第一步,不恥下問)
②如果這樣問:老師,這題答案是A,但我覺得是B。(這是經過思考的提問)
③最高境界的問法:老師能幫我看看這題,我的解法有什麼錯誤?(已經成形的高手,可以和老師對招了!)
這些年我常遇到的情況是:學生不是不會解題,而是不懂題目在問什麼!因為題目愈來愈長、愈來愈花稍、複雜、跨科、素養……,學生抓不到重點。所以,學生個別來找我問問題時,我會引導學生把題目的大意,用自己的意思表達出來,再從中檢視學生對題目瞭解的程度。很多時候,只要把題目講解一下,學生就會豁然開朗,馬上就能瞭解。閱讀能力的培養是最基礎的實力,學生的閱讀能力真的要再加強,尤其是篇幅較長的文章,要學會抓到重點。
至於國二升上國三的同學,會面臨一段極大的調適期,一邊要複習一、二年級的課程,還要學習三年級的課程。更恐怖的是,國二學過的理化怎麼變得好像都沒學過一樣,題目都好難!這是因為國二學的是入門,題目通常是比較基本的題型,但國三的複習題會進階,跨章節的整合性題目也會跟著出現,寫起來當然會有很大的挫折感。不只理化,其他國文、英文、數學、社會也都是如此,一邊複習、一邊衝進度。焚膏繼晷、蠟燭兩頭燒,實在很辛苦!這是所有國三學生都會遭遇的處境,只要跟著學校規劃的進度,不疾不除,一步一腳印,踩穩每一步,不放棄、堅持到底,相信一年之後,一定非同凡響!
【2022-10-24/聯合報/R06.07版/好讀周報動腦力】


、馮子晏(左二)、張詠捷(中)設計的水域自動充氣救生裝置,摘下世界發明展金牌。圖/記者張議晨-300x220.jpg)
