文/洪介興(教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中)
從情境 找待解問題 數學題 閱讀量增加
近年來,國中教育會考數學科題目的閱讀量大幅增加,從103年會考正式上路至今,選擇題的題數從27題逐漸減少到今年的25題,但題目的頁數卻不減反增,足以顯見閱讀能力的重要性日益提升。
細看歷屆的會考題,可以發現有一種題目,期待考生能從敘述較長的情境中,釐清已知條件與待解問題,接著找尋合適做法,正確解題。以今年的會考試題為例,選擇題25題當中有7題(題號9、11、14、16、18、24、25),以及2題非選擇題,都屬於這類題目,共占總分100分中的38.8分(選擇題每題為3.4分,非選擇題每1級分為2.5分)。
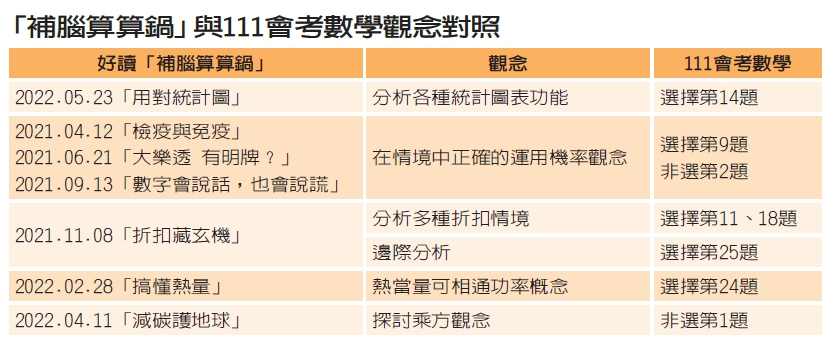
如果你是「補腦算算鍋」的忠實讀者,仔細看過今年的會考題目後,不難發現這些情境題所涉及的數學內容,幾乎都在本專欄文章中出現過。
全部情形是分母 題目問的是分子
選擇第9題以及非選擇第2題都是關於機率的情境題,只要弄清楚全部的情形(分母)有幾種、符合題目所求的情形(分子)有幾種,便能順利作答,以選擇第9題為例:

因為剩下的球全部是7顆,而其中有1顆1號、1顆3號、以及1顆5號,共3顆符合題目所求的「與小茹已抽出的5顆球中任意一顆球號碼相同」,因此機率便是7分之3。
這類關於機率的問題,在本專欄過去的〈檢疫與免疫〉、〈大樂透 有明牌?〉以及〈數字會說話,也會說謊〉這三篇文章中,都有深刻的探討。錯過這些文章的讀者不必扼腕,因為還是可以從「聯合學苑」網站上看到,在此也向讀者預告敬請期待未來其他機率相關的文章!
利用邊際分析法 比較有差異之處
去年11月好讀刊出〈折扣藏玄機〉一文,對購買商品常見的折扣方式,以及購買時的決策方法進行了種種分析,會考選擇第11題和第18題正是與折扣相關的問題。讀過這篇文章會更容易理解折扣問題的情境,不僅如此,文中所提的「邊際分析法」,更能用來幫助我們輕易地解決選擇第25題。
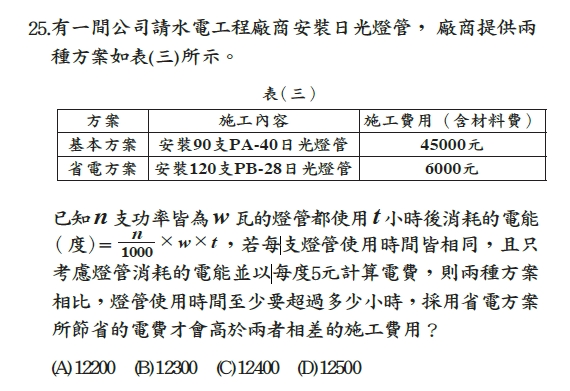
「邊際分析法」意指從兩種方案中選擇時,無視重複的部分,只針對有差異的地方比較。會考選擇第25題,最後一句中的「採用省電方案『所節省』的電費」和「兩者『相差的』施工費用」就是兩個方案有差異的地方,將它們進行比較即可,若熟悉邊際分析法的思考方式,讀完題目幾乎可以馬上作答:

考理解分析 計算量不多
會考選擇題的順序會盡量依照難度排列,前面的例子是選擇最後一題,屬於難度較高的題目,但計算量其實不大,難處只在於你能否從情境中判斷出正確的解題方法。其實不僅情境題如此,純數學題的計算量也都不大,以下我們以選擇第20題為例。
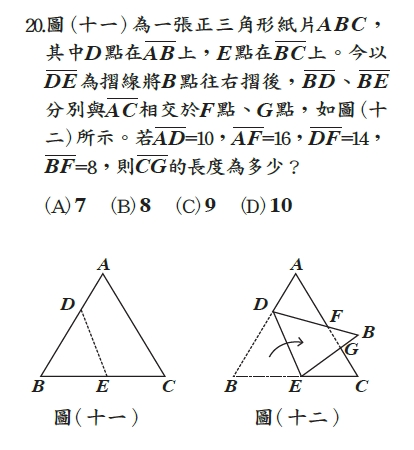
第一步是把AD、DF、FB的長度相加,得到正三角形的邊長是32。接下來,此題的關鍵就是要看出△ADF和△BGF是2倍的放大縮小圖,因此FG的長度是DF的一半,也就是7;最後只要用AC的長度,減去AF和FG的長度,就可求出CG的長度了。需要的計算僅有以下所示:

由以上幾題的例子中可以知道,破解會考題只需要很基本的計算能力,更重要的是閱讀理解能力、觀察推理能力、分析思考能力,這些更高層次的認知能力;這些能力無法靠著背誦公式、記憶題型、熟悉計算來獲得,而是藉由多閱讀、多觀察、多思考來增強。
因此,平常學習數學時,我們要做的不是把公式背起來,而是要能詮釋公式的意義;不是記憶例題的解法,而是要能說明每一個步驟;不是練熟題型和計算,而是能夠嘗試多種解題方法。
薪資圖 考題一模一樣 談賽局 作文也能引用
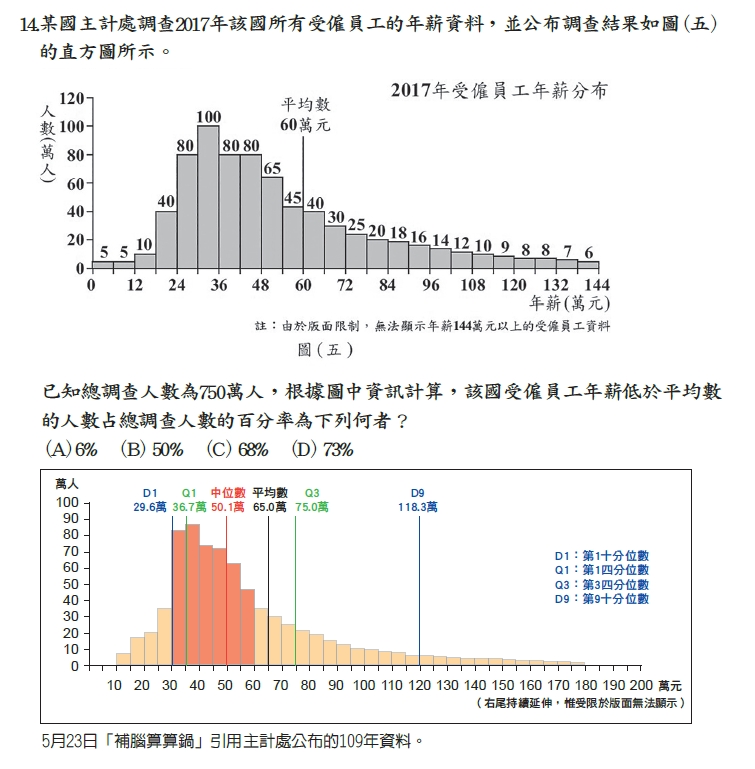
此外,還有一個絕佳的學習管道,那就是多讀「補腦算算鍋」的文章,培養閱讀與思考力!不知讀者們有無發現,5月23日刊出的〈用對統計圖〉中,出現了一張和今年會考題一模一樣的統計圖(差別只在於資料年份不同)!由此可見,本專欄和心測中心(會考命題的負責單位)真可謂英雄所見略同!
今年會考作文以「多做多得」為題,去年11月所刊出的〈賽局理論〉一文中,最後有段關於「自私」與「利群」的人性探討,這不就是絕佳的作文題材嗎?擷取其中一段:
「如果每個人都只在意自身的利益,這個群體必定走向滅亡,所幸絕大多數的人都還是會顧慮到群體的利益,都有責任感、有榮譽心、有大愛,都願意付出自己的一小份心力讓社會變得更好,除了利己、更能利他,甚至把群體的利益排在自己之前,這正是人性的高貴與美麗,也是真正能推進人類文明的動力。」
原來閱讀「補腦算算鍋」,不僅能提升數學素養,還能充實作文的題材啊!
原文出自《好讀周報》671期