文╱洪介興
●問問你╱黃金分割是什麼 黃金比例是多少
給你一條繩子,請你把它分割為長短不同的兩段,目標是要讓這兩段繩長的倍率關係,恰好等於較長一段的繩長和原本長度間的倍率關係,這件事有可能辦得到嗎?
這裡我們需要考慮兩個倍率,第一個是切開的兩段繩子中,長段長除以短段長的倍率。如果切開的位置越靠近中央,這個倍率就會越接近1,最小不會低於1;而如果切得越靠邊,這個倍率就會越大,甚至可以無止境地大。長段長與此倍率間的關係如圖一所示。
第二個要考慮的是全長除以長段長的倍率。如果切開的位置越靠近中央,這個倍率就越接近2,最多不會超過2;而如果切得越靠邊,這個倍率就會越小,最小不會低於1。長段長與此倍率間的關係如圖二所示。
將兩個倍率放在同一個關係圖中(見圖三),看起來應該會有一個恰恰好的分割方式,可以讓兩個倍率剛好相等。事實上,這個「不多不少剛剛好」的美麗分割方式確實存在,它有個厲害的名字,叫做「黃金分割」,而黃金分割所得到的倍率就稱為「黃金分割率」,亦常作「黃金比例」,其值為1.61803……,小數部分無窮無盡且沒有循環規律,一般以希臘字母「φ」(讀作ㄈㄞˋ)表示之。
●有意思╱黃金切割黃金矩 黃金螺線就會成形
用剛才我們作黃金分割的繩子全長,以及分割後的長段,當作矩形的長、寬,會形成一個長寬比正好是黃金比例的矩形;或是用分割後的長段和短段,當作矩形的長、寬,也會得到長寬比正好是黃金比例的矩形。像這樣長寬比符合黃金比例的矩形,就稱為「黃金矩形」。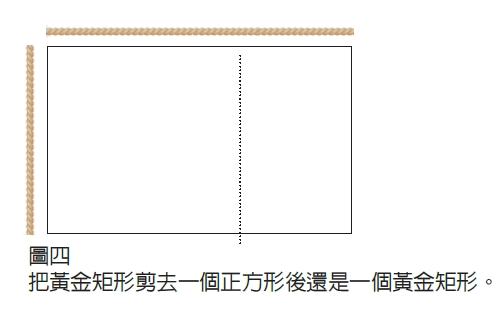
把上面兩個黃金矩形對齊重疊在一起,就會看到一個很厲害的性質:把黃金矩形剪去以自身短邊為邊長的正方形後,剩餘的部分仍然會是一個黃金矩形。這是因為剪去以短邊為邊長正方形的這個動作,恰好就是對原矩形的長邊進行黃金分割。且更有趣的是,這個動作可以不限次數地一直進行下去。
不斷進行上述的切割,並在每個正方形內畫上一條四分之一圓弧,會形成一條等角螺線,而像這種以黃金比例作為增長因子的等角螺線,稱為黃金螺線,自然界中小至鸚鵡螺,大至颱風、甚至銀河,都可以看到它的蹤影。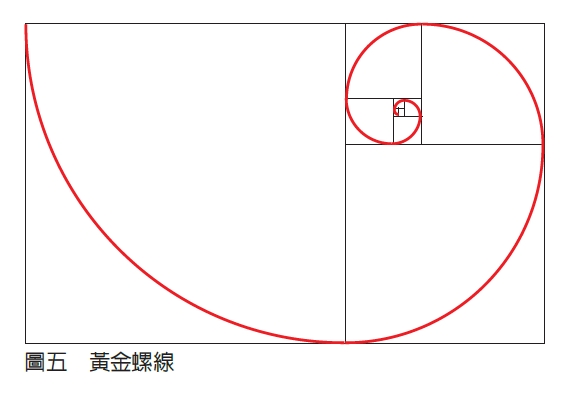
●告訴你╱正五邊形很特別 對角線多黃金比例
正五邊形有著非常特異的性質,除了對角線和邊長的比值正好是黃金比例外,當我們把五條對角線都畫出來後,會出現更多的黃金比例,事實上,圖中每條線段的長度,都能找得到其他長度與其形成黃金比例。
圖中可以找到許多大大小小不同的兩種等腰三角形,其中一種是3個內角度數36度、72度、72度的銳角三角形,另一種則是36度、36度、108度的鈍角三角形。這兩種三角形都叫做黃金三角形,原因是它們長短兩種邊長的比值都是黃金比例。更有趣的是,從圖中還可以發現,一個銳角的黃金三角形和一個鈍角的黃金三角形,竟然可以合併成一個更大的黃金三角形!
●再問你╱棋子路過10格 會有幾種路徑
下圖中有10個格子,最左邊的第1個格子中有一個棋子,讓這個棋子順著箭頭移動,當有兩條路的時候,可以任意選擇其中一條路前進,一直走到最右邊的第10個格子,總共會有幾種不同的路徑?
試著把走到該格的路徑數填在每一個格子裡,第1格先填1;走到第2格顯然只有1種路徑,所以也填1;走到第3格有2種方法,所以填入2;走到第4格有3種方法,所以填入3,你可以驗證看看前面的敘述是否正確。
到了第5格,就不要一條一條路徑慢慢試了,可以直接把第4格和第3格內的數字3和2相加,將5填入第5格內。這是因為走到第5格的路徑可區分成兩類:一類是從第4格走過來,因為走到第4格有3種路徑,所以從第4格進入第5格的路徑就是3種;而另一類是跳過第4格,從第3格直接一步抵達,因為走到第3格有2種路徑,所以從第3格直接進入第5格的路徑就是2種;因此,走到第5格的路徑數就是這兩類的總和,也就是5種。
根據同樣的道理,可知道抵達第6格的路徑數,就是到第5格和到第4格的路徑數總和,也就是8;抵達第7格的路徑數就是8+5,也就是13;而第8格是21、第9格是34、第10格就是55。
●看原理╱何謂「費氏數列」 每個數是前兩數總和
前兩個數是1,接下來的每一個數是前兩個數的總和,依此規則形成的數列叫做「費波那契數列」,簡稱費氏數列,這個數列的前幾項為:1、1、2、3、5、8、13、21、34、55、89、144、233、377、610……,可一直不斷地延伸下去。
費氏數列是以13世紀的義大利數學家,比薩的李奧納多(Leonardo Pisano Bigollo)的外號「費波那契」為名。此數列其實是由印度數學家所發明,費波那契對其進行研究,並使歐洲人知曉。費波那契最大的貢獻是把印度阿拉伯數字引入歐洲,對西方的科學產生了深遠的影響。
費波那契數列的生成方式很簡單,卻蘊含豐富的有趣性質。舉例而言,數列中每一項的平方,都和相鄰兩項的乘積相差1,譬如52和3×8相差1、82也和5×13相差1,讀者不妨多找幾個數驗證看看,更能感受其奧妙。另外,在648期介紹過的帕斯卡三角中,也能找到費氏數列的蹤跡,是否相當神奇呢?
●很神奇╱螺旋結構的植物 常常出現「費氏數」
你心中是否有個疑問,為什麼黃金比例講著講著,會突然跳到費氏數列呢?這是因為費氏數列有一個非常美麗的重要性質:相鄰兩項的比值會趨近於黃金比例(見表一)!也因此,費氏數列又有「黃金數列」之稱。
費氏數列中的數稱為「費氏數」,正如同黃金比例一般,費氏數也常在大自然中出現,尤其是在有螺旋結構的植物上,像是花瓣多為5瓣,在松果和鳳梨上可看到8或13股螺線,而在向日葵上可看到21、34、甚至55股螺線,令人不得不折服於大自然造物之奇!
原文出自《好讀周報》650期