文╱洪介興
●考考你╱左上角→右下角 走法總共有幾種
圖一中有一個2列3行的方格,左上角的格子中有一顆棋子,現在要將這顆棋子一格一格地移到右下角的格子,規則是每一步只能往右或往下走,且不能斜走,如此總共會有 3種不同的路徑。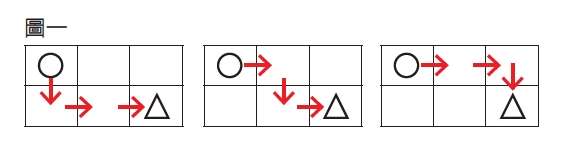
接下來請你試試看,如果換成是3列4行的方格,依相同規則把棋子從左上角移到右下角會有幾種不同的路徑?而若換成是4列5行的方格,又會有幾種不同的走法呢?
你試出來了嗎?如圖二所示,在3列4行 的方格中,總共可以找到10種不同的路徑,若你能全數找出,可說是相當厲害!但換成4 列5行時,就相當不容易了吧?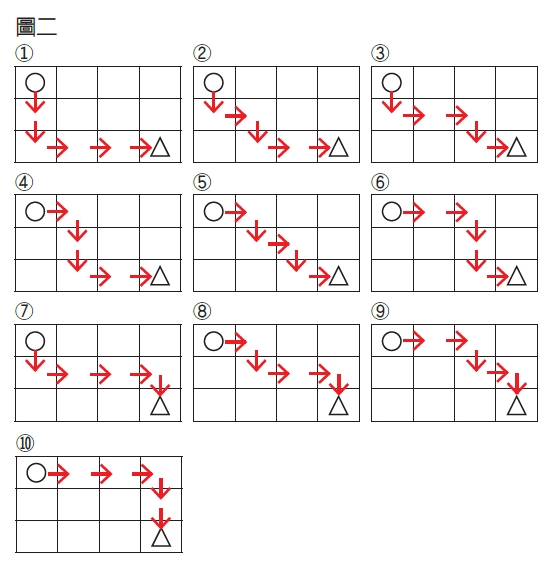
●看訣竅╱格子內的數字=所有可能路徑數
不好意思,當你還在焦頭爛額之際,我已經用一個快速的算法,求出在4列5行的方格中,總共可以找到35種不同的路徑。方法是 先在最上列和最左行的所有格子中填入1,剩下的空格從左上角起填入數字,填入的數要是上方和左方兩個數的總和。每個格子內的數都是代表從起點走到該格的路徑數,因此右下角格子中的35,就表示走到右下角總共有35種不同的路徑。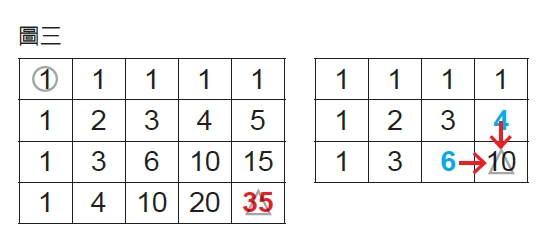
至於為什麼每個格子內的數,都正好會是從起點走到那一格的所有可能路徑數呢?
首先,如果是要走到最上面一列或最左邊一行的格子,由於完全沒有轉彎的可能,所以都是單一路徑,因此這些格子內都應該填入1沒錯。
再來,對其他的格子而言,若要走到該格,最後一步可能是從左邊來的,也可能是從上面來的。以走到第3列第4格的10種路徑為例,這10種路徑可以分解成從左邊來的6種(即圖二中的第1種~第6種路徑),和上面來的4種(即圖二中的第7種~第10種路徑),所以對於任一個格子而言,走到左邊格子的路徑數,加上走到上面格子的路徑數,就是走到該格的路徑總數。
●告訴你╱帕斯卡三角形 暗藏數學驚喜
接下來介紹一個非常美麗的數學構造,稱為帕斯卡三角形(如圖四),此三角形是以法國數學家布萊茲帕斯卡(Blaise Pascal, 1623~1662)為名。但根據文獻記載,11世紀的北宋數學家賈憲更早提出這個結構,因此也稱做「賈憲三角形」。回到帕斯卡,他同時也是物理學家、化學家,壓力單位帕斯卡(Pascal)便是以他為名,以紀念他在該領域研究的貢獻。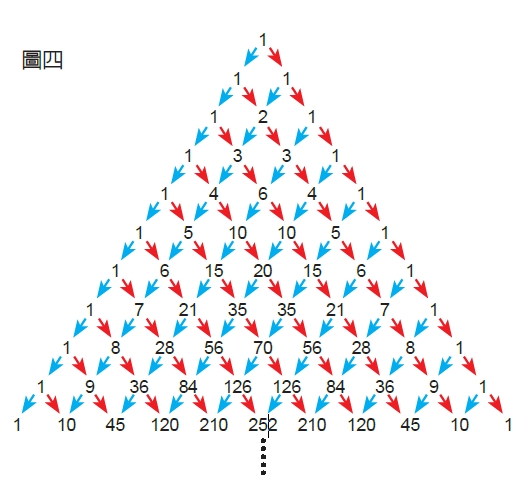
帕斯卡三角形的頂端是1,往下每一列會比前一列多1個數,並交錯排列,每個數都是上方的左、右兩個數的總和,而最旁邊的數,因為上方只有一個數,所以會維持在1。
我們會說帕斯卡三角形美麗,指的當然不只是外觀上的美,更重要的是數學上的美。首先,你很可能已經發現,帕斯卡三角形的結構只是把我們前面提過的路徑數問題轉個方向擺放,並加以無限延伸,接下來看看帕斯卡三角形能帶給我們什麼驚喜。
●性質1╱第3斜行為三角形數 第4斜行是三角垛數
我們把從頂端一路往右下稱為第1斜行,從第二列左端的1一路往右下稱為第2斜行 其次是第3斜行、第4斜行,第1斜行剛才說過永遠是1,而第2斜行則是連續的自然數1、2、3、4……看起來有點意思了,更厲害的還在後頭。
再看到第3斜行,是1、3、6、10、15……,這個數列名為三角形數,意思是將物品排列成三角形,一層一層增加的全部總個數。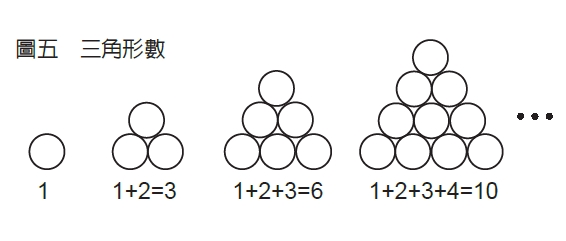
再來到第4斜行,你會看到1、4、10、20、 35……,這個數列名為三角垛數,意思是將物品堆疊成三角垛,一層一層增加的全部 總個數。帕斯卡三角形中竟然蘊含了這麼有趣的數列,是不是很不可思議呢?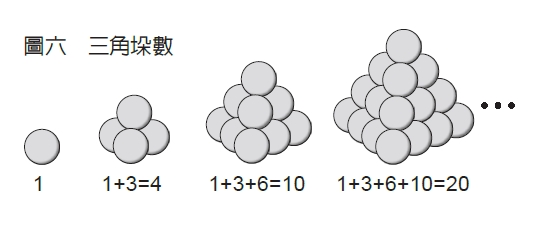
之所以會有這樣的現象,原因如下:首先要瞭解,三角形數可由1+2+3+4+…而得,而第2斜行上的1、2、3、4……等數,正好會因為帕斯卡三角形的加總規則,而彙集在第3斜行的同一格中,如此便形成一個又一個的三角形數。
至於三角垛數,則可由三角形數1+3+6+10+…加總而得,而第3斜行上的三角形數們,同樣會彙集到第4斜行上的同一個格子內,形成一個又一個的三角垛數。當然第2斜行上的1、2、3、4……等數,也可以看成是由第一斜行的1、1、1、1……加總而來。
●性質2╱每一橫列的數 =(x+1)n的各項係數
下一個厲害的性質是:如圖七所示,每一橫列的數,正好都會形成(x+1)n的各項係數!這又是什麼原因呢?讀者不妨先試著觀察、思考一番,再往下繼續閱讀。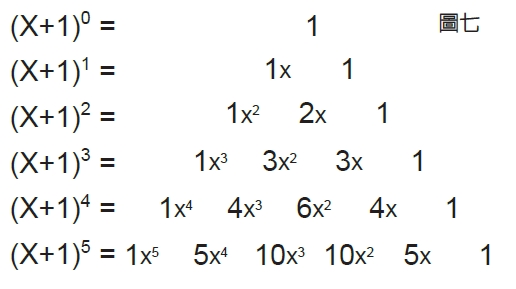
為了方便說明,我們先規定頂端叫做第0列,下一層叫做第1列,再下一層叫做第2列,以此類推。
以第4列推到第5列為例,假如我們已經確定第4列的數依序都是(x+1)4的各項係數,也就是說(x+1)4=x4+4×3+6×2+4x+1,現在我們要計算(x+1)5,看看係數變化是不是正好符合帕斯卡三角形的運算規則。
由圖八、圖九的推導可以明顯地看出,只要確定第4列的數依序是(x+1)4的各項係數,下一列,也就是第5列的數也必定會依序是(x+1)5的各項係數。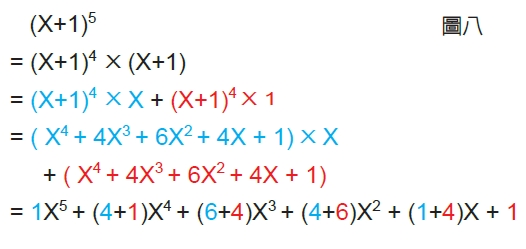
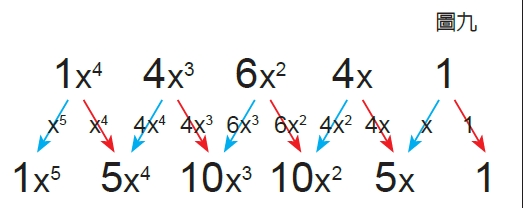
事實上,前面這個推論方式可以適用在從任何一列推到下一列,像我們剛才確定了第5列的數依序是(x+1)5的各項係數,那麼根據同樣的推論方式可知,第6列的數也必定會依序是(x+1)6的各項係數。同樣地,第7列、第8列、第9列……等後續的每一列都必然會符合這個漂亮的性質。
●想想看╱7張牌挑3張牌 總共有幾種組合
有A、2、3、4、5這5張牌,請你從中挑選2張牌,譬如A2、A3、25、45……,請你算算看總共有幾種不同的組合。
如果你是有系統性地找,應該很快就可以得出是10種組合。再考考你,若從A、2、3、4、5、6、7這7張牌中挑選出3張牌,這樣總共有幾種不同的組合呢?
即便你是很有系統性地找,恐怕也不是這麼容易吧!不好意思,這裡我又有一個快速算法:直接查帕斯卡三角形,第7列的第4個數,35就是這題的答案!這是因為選牌組合數問題,和本文一開始提到的路徑數問題,看似截然不同,其實卻是相同的問題!
我們以3列4行的路徑問題為例,每一條路徑都是總共走5步,其中2步向下走,3步向右走,所以可以用2個「↓」和3個「→」的排列來表示每一種路徑。而這又可以看成是:從編號1~5的5個格子中,挑選其中2個格子畫上「↓」,剩餘的畫上「→」,看有幾種不同的選法。這就跟從A~5當中挑選2張牌是相同的意思了,而我們前面又說過帕斯卡三角形的構築跟路徑數問題相同,只是轉了一個方向,所以選牌組合數問題的答案可以在帕斯卡三角形中找得到
帕斯卡三角形裡面還有許多漂亮性質,譬如每一列的總和都是2的次方(詳細理由請讀者試著想想看,關鍵在於前一列的每個數都會被下一列用到2次),說也說不完的。你看,如此簡單的生成方式,卻能築出蘊含如此豐富性質的結構,你說,帕斯卡三角形是不是很美呢?
●作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中
原文出自《好讀周報》648期




