文╱洪介興
●說緣起╱較大的數怎處理 進位系統來幫忙
我們都知道0的下一個整數是1,1的下一個整數是2,接下來是3、4、5、6、7、8、9,但再下一個整數就沒有它自己獨有的符號了,而是由1和0組合而成的「10」。
為什麼不繼續發明獨立的新符號來代表下一個整數呢?這是因為一來,我們無法記住太多符號;二來,整數可以無窮地延伸,不可能無止盡地發明新符號。因此,若想處理較大的數,進位系統就是必要的存在。
有人可能會想到:如果接下來要發明的新符號都用舊符號進行組合,這樣就不會增加記憶負擔,而且只要組合的規則制定得宜,應該可以無限地延伸,雖然可能會筆劃很多、寫得很擠,但至少是有辦法的啊!
如果能想到這一層,表示你的數學造詣頗高;但其實任何用舊符號進行組合的方法,仍然都是一種進位系統,只是用了不同的呈現方式來表達出進位的效果而已。
●想想看╱合理的進位制度 最小規定幾進位
我們生活中所使用的進位系統是十進位制,在這個制度下,「十」這個數沒有自身獨有的符號,而是用左邊一位的「1」來表現;那麼,我們有沒有可能創造更多獨立的數字符號,這樣就能碰到更大的數字再進位;或是不要使用這麼多的數字符號,在還不到十的時候就進位呢?
我們現在試著用「A」表示9的下一個數,它等同於十進位下的10;再用「B」表示A的下一個數,它等同於十進位下的11;接下來的四個數是「C」、「D」、「E」、「F」,分別等同於十進位下的12、13、14、15;新符號到此為止,「F」的下一個數就進位用「10」表示,這個數相當於十進位下的16。
在這個進位制度下,「十六」這個數沒有自身獨有的符號,而是用左邊一位的「1」來表現,由於這個進位法是逢十六進位,故稱為十六進位制。順帶一提,十六進位制下的「10」要讀做「一零」比較合適,避免與十進位制的「十」混淆。
使用上述的十六進位制,進行數數的時候就會像圖一。
如果甲、乙兩人用同樣的時間間隔,同時從0開始進行數數,但甲用的是十六進位制,而乙用的則是十進位制。那麼當甲數到「100」的同時,乙會數到「256」。也就是說,十六進位下的100,和十進位下的256,表象雖不同,但本質上指的其實是同一個數。
看完十六進位制的例子,你應該不難想像其他像是十二進位、八進位、五進位等不同進位制了吧,譬如用五進位制來數數就是:0、1、2、3、4、10、11、12、13、14、20、21……。接著考考你,一個合理的進位制度,最小可以規定成幾進位呢?
●考考你╱十進位制的250 二進位需幾位數?
有想法了嗎?現在公布解答—進位法最小可以規定到二進位,用二進位制數數就是:0、1、10、11、100、101、110、111、1000、1001、1010、1011、1100、1101、1110、1111、10000、……。由上觀察可知,二進位下的「10000」等同於十進位下的16。
在二進位下要用到5位數才能表達十進位下的16,感覺似乎很沒效率,現在請你猜猜看,若使用二進位制,要表達出十進位制的250需要多少位數?又,要表達出十進位制的60000需要多少位數?
在深入探討這個問題之前,且讓我們先跳到中國古代流傳下來的易經,看看二進位法是怎麼體現在易學中的。
●看易經╱八卦=3個爻的組合 64卦=6個爻的組合
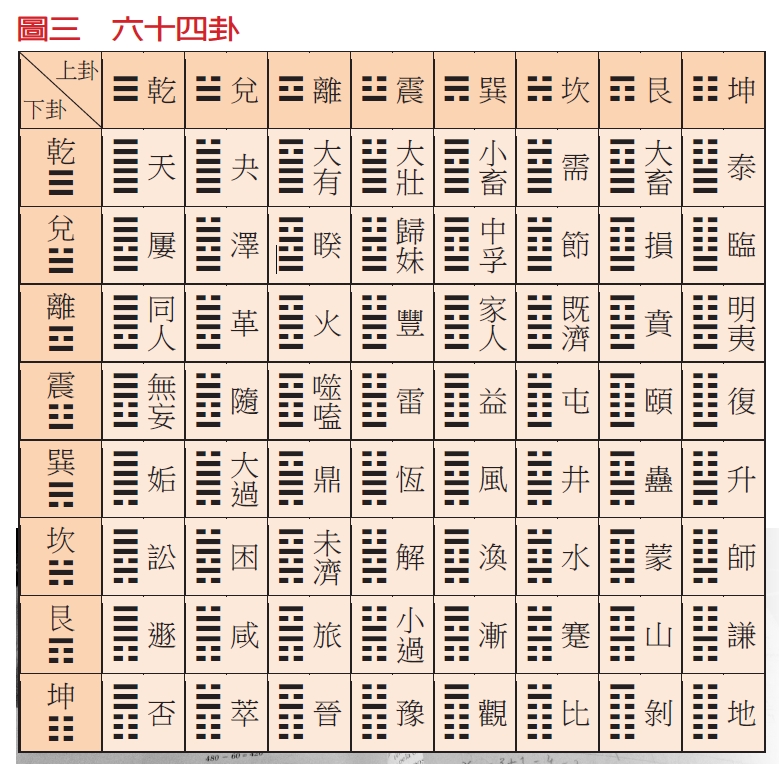
《周易.繫辭》中記載道:「易有太極,是生兩儀,兩儀生四象,四象生八卦。」其中兩儀是「陽儀」與「陰儀」;陽儀再多加一次陰陽屬性,便可分得「太陽」、「少陰」,而陰儀則可分得「少陽」、「太陰」,此為四象;而四象又可各自再多加一次陰陽屬性,分得「乾、兌、離、震、巽、坎、艮、坤」等八卦;最後再將兩個八卦上下相疊,便可得到六十四卦。
讓我們來分析一下八卦和六十四卦的數學結構:八卦的每一卦都是由3個爻所構成,每個爻都是陽爻或陰爻兩者的其中一種,因此共有2×2×2,也就是23,即8種可能的組合,所以八卦其實就是3個爻的所有可能組合;而六十四卦的每一卦則是由6個爻所構成,因此共有26,即64種可能的組合,所以六十四卦就是6個爻的所有可能組合。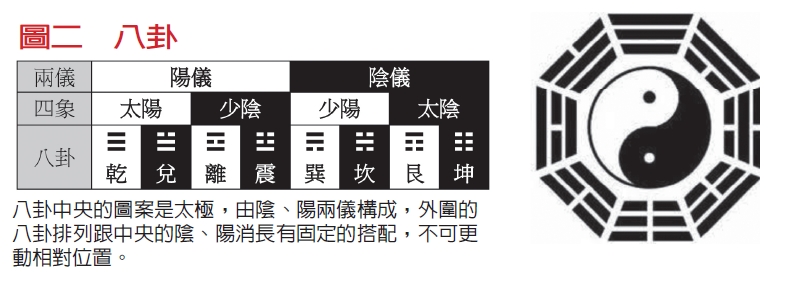
●看應用╱資訊運算靠二進位 磁碟讀寫也二進位
現在讓我們回到二進位制的討論,你是否有發現:剛才對八卦和六十四卦所進行的數學分析,完全可以類比到二進位制的探討呢?
因為每一個位數都是0和1兩種可能,所以8位數會有28,即256種組合,可對應到十進位下的0至255;而16位數會有216,即65536種組合,可對應到十進位制下的0至65535。現在我們可以回答之前的問題了:在二進位下,用8位數可表達出十進位的250(即11111010),而十進位的60000則需要16位數(即1110101001100000)。
在現今這個數位時代中,二進位法其實正無時無刻地服務我們,因為所有的資訊裝置幾乎都是靠二進位法運作的。你可能會好奇:為什麼資訊設備都要倚賴二進位法呢?在回答這個問題之前,請你先試著想想看:要怎麼用電線傳輸一個數,甚至一個中文字呢?
方法是先把待傳輸的資料轉成二進位,然後用高電壓表示1、低電壓表示0,接收端就可以從電壓的訊號讀出二進位的訊息,最後再轉換回原本的資料即可。其實不光是傳輸,磁碟也是利用磁的二極性來記錄二進位的資料。至於運算,不論是加法還是乘法,二進位的運算表都非常簡潔,如此便能用電子電路的邏輯元件輕易表達。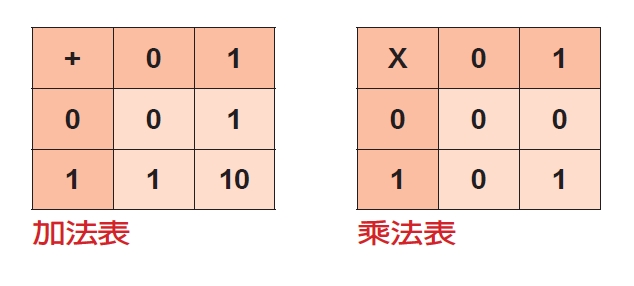
●告訴你╱中文 2Bytes進行存取 圖片 3Bytes表三原色
十進位制的數可轉成用二進位制表示,這還不難理解,然而,文字、甚至圖片要怎麼用二進位的數表示呢?
首先我們要認識bit(位元)和Byte(位元組),每一個0或1稱為一個bit,而8個一組的位元稱為一個Byte;單一個Byte可以儲存256種不同的資料,而2個Bytes則有65536種不同的變化。中文字就是用2個Bytes進行存取的,譬如「數」這個字,電腦會把它記錄成「01100101 01111000」。
至於圖片,以一張高畫質(HD)的照片為例,畫面會是由1080行乘以720列的小小方格(像素)所構成,每一個方格用3個Bytes記錄其顏色,這3個Bytes分別記錄光的三原色──紅光、綠光、藍光的強度,在一些可選擇顏色的電腦程式中(如:小畫家、Word),你只要選擇「自訂色彩」,就可以試著調整紅、藍、綠的數值(0~255),看看調出來的顏色如何,相當有趣喔!
根據前一段的說明,我們可以計算出一張HD的照片,是由1080×720×3×8,也就是大約2千萬個0或1所構成。單純的0或1竟然可以表現出電腦中這麼多彩的內容,是不是很不可思議呢?
●作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中
原文出自《好讀周報》646期