[補腦算算鍋] 公車多久來？

文╱洪介興

●狀況1╱班距20分鐘平均須等10分鐘

只要你搭過公車，一定知道公車站會張貼所有經過路線的乘車資訊。除了每個路線經過的公車站，乘客們普遍會注意的資訊就是班距，因為這關係到等車所需的時間。

想像以下的情境：我們要一起搭乘A路公車去參加聚會，到公車站後你看了看乘車資訊，發現班距是20分鐘。這時候，你會「預期」要等多久？是20、15，還是10分鐘、5分鐘？你認為怎樣的預期最合理呢？

要回答這個問題，就必須把各種可能都想清楚。

如果前一班公車才剛走1分鐘，那麼我們得等19分鐘才能等到下一班公車；如果前一班公車已離開2分鐘，則我們要等18分鐘；如果前一班走了3分鐘就是等17分鐘；最理想的狀況，是前一班公車已經離開了19分鐘，這樣只要等1分鐘就會等到下一班車了！也就是說，等待時間從1分鐘到19分鐘都有可能。

如果上述每一種狀況發生的可能性都一樣，也就是所有狀況發生的機會均等，這時「平均數」就是非常好的估計方式：因此將上述所有可能的等待時間平均為10分鐘，就是合理的「預期」等待時間。（如圖1）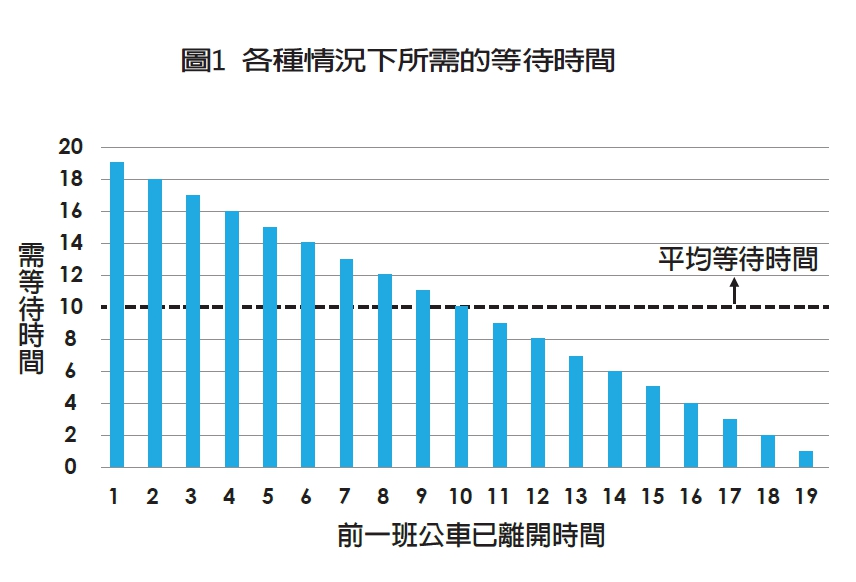

●狀況2╱已等4分鐘只須再等6分鐘？

討論到這裡，時間已經過了4分鐘，公車還沒來，這時候你預期我們還要再等多久？

原本我們預期等10分鐘，因為經過了4分鐘，所以你現在會預期還要再等6分鐘？這個很直接的想法，卻會把我們導向錯誤的結果，原因是錯把「或然」當成了「必然」。

剛才我們所預期的10分鐘等待，只是用一個數來代表所有或然的狀況，並非必然會等10分鐘。如果公車抵達時間是確知的，直接相減是正確的，但碰上這種有不確定性狀況時，正確的做法是加入新資訊一起考量，重新進行估計。

因為我們已經等了4分鐘，所以從一開始「只須等待4分鐘以內」的狀況都不可能發生了，剩下的是等待5分鐘、6分鐘、7分鐘直到等待19分鐘的狀況，扣掉已經過了的4分鐘，意味著還要再等1分鐘、2分鐘、3分鐘……15分鐘，平均還需要的等待時間是8分鐘，而非直接「10減4」。

●狀況3╱如有兩班車理想狀態等5分

歡樂的聚會活動雖結束，但美好的時光尚能延續，因為我們還是要一起搭公車回去，可喜的事還不只一樁，除了A路公車外，回程還多了同樣是每20分鐘發一班車的B路公車可以帶我們回去。我們來的時候預期等10分鐘，現在可以搭的公車多出了一倍，是否能為我們省去一半的等候時間呢？

B路公車帶給我們的效益多大？這個問題其實是取決於B路公車和A路公車的抵達時間相隔多久。

最理想的狀況是B路公車和A路公車抵達的時間正好相距10分鐘，在這樣的狀況下，這兩路公車合起來正好形成固定10分鐘的班距，那麼預期的等待時間也會減半為5分鐘。（如圖3）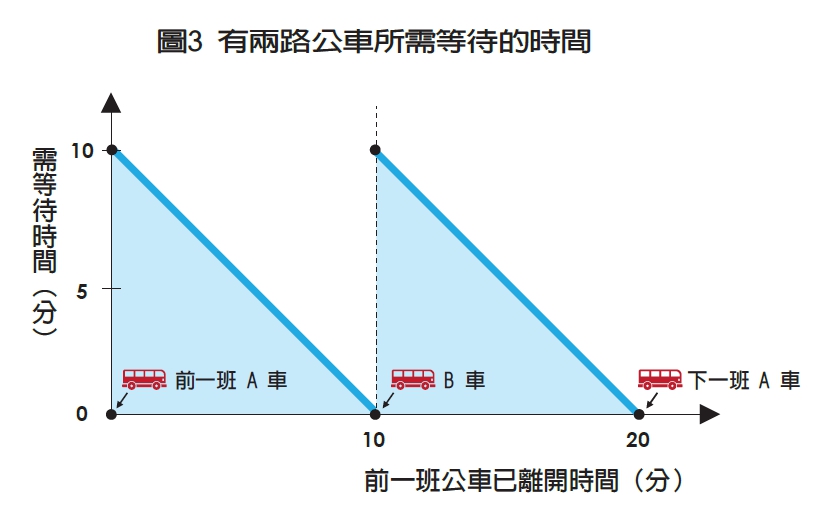

●再想想╱除考慮狀況發生機率也計算

但最差的狀況也是有可能發生的，那就是B路公車和A路公車的抵達時間正好相同。在這樣的狀況下，多出來的B路公車完全不會為我們省下任何一點時間，預期的等待時間仍為10分鐘。

然而還有其他可能狀況要考慮，如果B路公車固定在A路公車離開4分鐘後抵達，則兩路公車合起來看的班距就是4分鐘、16分鐘、4分鐘、16分鐘……。如果我們是在A路公車剛離開、而B路公車尚未到站的這4分鐘內到公車站開始等車，需要的平均等待時間是2分鐘；但若我們是在B路公車離開後、A路公車到站前的16分鐘內等車，需要的平均等待時間則為8分鐘。

上述兩種狀況都可能發生，我們可能只要等2分鐘，也可能要等8分鐘，但這次我們不能直接把這兩個數字取平均。因為我們有比較高的機率是在B公車離開後的16分鐘內開始等車，而在另外4分鐘內開始等車的可能性則較低。所以計算平均的時候要分給等8分鐘的狀況比較高的比例，分給等2分鐘的狀況比較低的比例，計算結果是6.8分鐘，平均等待時間仍是介於8分鐘和2分鐘之間，但並不是正中間的5分鐘，而是會比較偏向8分鐘。（如圖4）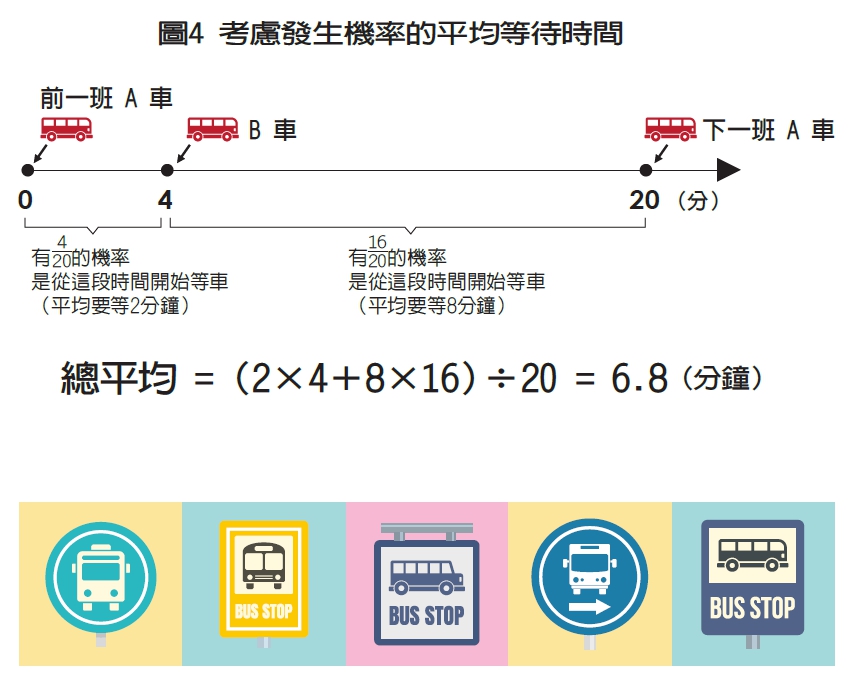

●有可能╱多一班公車只省1/3時間

最後，由於我們不知道兩路公車的抵達時間相隔多久，所以還需要考慮各種可能情形再加以平均。（如附表）

如果你有注意到附表中其實並沒有真正地考慮到所有情形，這表示你的覺察力非常敏銳喔！事實上，若考慮到每1分鐘的情形，就可得到更準確的數據6.675分鐘；而若考慮到每0.5分鐘的情形，則會算出6.66875分鐘；如果要考慮到每一瞬間的無限多種情形，那就必須藉助微積分的力量了，可得出的計算結果是6又2/3分鐘，結論是多出這一倍的車量，其實只為我們省下了1/3的時間。

「咦？剛剛走掉的是不是B路公車啊？」

「啊！好像是耶！」

畫面中只見揚長而去的公車，和專注於思考而沒留意公車的兩人。