2022聯合學苑「夏令營 ● 夏季班」6/20最後優惠日!
文╱洪介興
●問問你╱圓周長與直徑比 圓周率怎算出來的
我們都知道圓周率是圓周長和直徑的比值、大約是3.14,也就是說任何圓的圓周長都是直徑的3倍多一些,但你有沒有深入想過,這個倍率是怎麼得到的呢?
圓周是彎曲的,難以跟直徑比較長度,因此先用多邊形來幫助我們進行探討或許會是個好辦法。
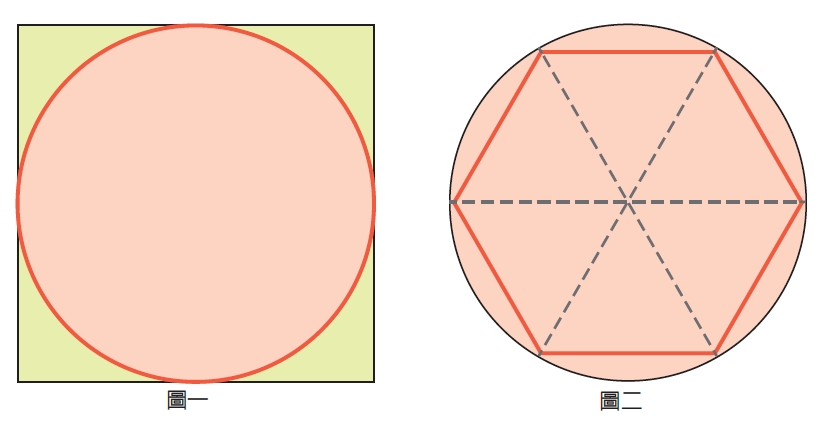
圖一是一個圓形和圓外接正四邊形,此正四邊形的邊長正好等於圓形的直徑長,所以正四邊形周長是圓形直徑長的4倍,圓周長顯然比正方形周長還短,可知圓周長明顯不到直徑的4倍。
圖二是一個圓形和它的圓內接正六邊形,正六邊形有個很厲害的性質,就是它恰好可以分割成6個完全相等的正三角形,因為這些三角形的邊長都等於圓形的半徑長,所以此正六邊形周長正好是圓形半徑長的6倍,也就是直徑長的3倍。再由觀察可知圓周長比正六邊形的周長略長,因此圓周長就是直徑長的3倍多一些,這張圖巧妙地驗證這個事實,是不是很漂亮呢?
●看歷史╱阿基米德最早計算 祖沖之推到小數七位
經過前面的分析,我們只能確定圓周率比3略大,但要如何得到更準確的數值呢?一個可能的方法就是實際測量,然而這麼做免不了會有不小的誤差。
在一塊西元前1900年至1600年的泥版上,揭示了古巴比倫人把25/8(也就是3.125)當作圓周率的證據,此數值很可能是經由實際測量、化約而來,相較於圓周率的真實數值,誤差大約是0.53%,如果用這個數值去計算直徑10公尺的圓周長,大約會低估16.6公分。這個誤差雖然不是非常大,但總是不讓人滿意,如果想得到精確的圓周率,還是必須用算的才行。
人類計算圓周率的歷史,最早可追溯到古希臘最偉大的科學家阿基米德(西元前287–212年),他一生所做的研究不計其數,在數學、物理學、工程學、天文學皆有極高成就,並和牛頓、高斯被合稱為史上三大數學家。阿基米德算出圓周率的值介於223/71和22/7之間(約為3.1408~3.1429),用這個範圍的數值當作圓周率最多只會有0.04%的誤差。
500年後,東方出現了另一位圓周率發展史上極具代表性的人物:三國時代魏國的數學家劉徽(約西元225–295年),他用了和阿基米德類似的方法,求出圓周率介於3.1410~3.1427之間。200年後後,南北朝劉宋的數學家祖沖之(西元429–500年),承襲了劉徽的算法,更是把圓周率的近似值準確求到前7位小數──3.1415926,這個數值只有億分之2不到的誤差,如果用這個數值去計算直徑10公尺的圓周長,誤差不超過萬分之1公分,也就是1微米,連一個細菌的大小都不到!
●看原理╱N邊形的N越大 圓周率誤差越小
你一定會想知道阿基米德跟劉徽是怎麼計算圓周率的,因為圓周率是圓周長和直徑長的比值,所以只要先任意決定直徑長(直接定為1最為方便),接著計算出這個圓的周長,然後將求出的圓周長除以直徑長就是圓周率了。但問題來了,圓周這種彎彎的線條,長度有辦法計算嗎?
我們前面有用過一個圓內接正六邊形的周長來跟圓周長做比較,發現圓周率比3大。阿基米德跟劉徽也是從這張圖出發,而接下來的動作,是往外畫出圓內接正12邊形,運用畢氏定理(直角三角形的三邊長之間的關係),計算出正12邊形的邊長,再乘以12,可得出此圓內接正12邊形的周長約為3.1058。
相較於圓內接正六邊形,圓內接正12邊形的周長顯然更接近圓周長。請你看著圖三,試著想像再往外畫出圓內接正24邊形、再往外畫出圓內接正48邊形、再往外畫出圓內接正96邊形……,當邊數細分到越多,得到的周長就會越接近圓周長,當邊數細分到非常非常多,得到的周長就會非常非常接近圓周長!
劉徽發明的割圓術,由祖沖之發揚光大,他由圓內接正六邊形的邊長求出正12邊形的邊長,再由正12邊形求出正24邊形的邊長;再由正24邊形求出正48邊形的邊長……,經過11輪的運算,得到圓內接正12288邊形的周長,進而將圓周率計算到小數第7位。
祖沖之所締造的紀錄高懸了近千年,才在西元1424年被波斯數學家卡西打破,他用割圓術算出圓內接正6×227邊形的周長,將圓周率推進到小數第16位;而割圓術最終的紀錄停留在1630年,由奧地利天文學家格林伯格將圓周率求到小數第38位。
●看發展╱無窮級數當解方 取項越多越準確
隨著17世紀微積分的蓬勃發展,數學家們開始找到許多可以表現圓周率的無窮級數,所謂無窮級數就是有無窮多項相加的算式,下面附上兩個例子。
你應該會感到驚訝,何以看起來如此簡單,且跟圓形看不出半點關係的算式,竟然能求出圓周率,實在太不可思議!
在這些圓周率的無窮級數中,只要往後面加上越多項,得到的圓周率就越準確,但是這兩個級數誤差變小的速度都太慢了,若要更加提升圓周率的計算速度,就要找到收斂速度更快的級數。
今年8月,瑞士格勞賓登應用科技大學的研究團隊宣布,他們花了108天的時間,用超級電腦將圓周率計算到小數62.8兆位,將圓周率計算的世界紀錄再度向前推進。該團隊所使用的計算方法,是由楚德諾夫斯基兄弟於1987年所提出的公式,這個級數收斂的速度極快,每多加上一項就可以多得到大約14位小數,效率高得非常驚人!
●問題1╱能否破解圓周率 目前來說不可能
圓周率有幾位小數?我們會有算出圓周率的一天嗎?很可惜地,以目前人類所知的數學知識看來,答案是不會。
1761年,瑞士數學家朗伯已經證明了圓周率不是有理數,也就是說圓周率無法表示成分子、分母皆為整數的分數,當然也就不會是有限位數的小數了,圓周率若以小數表示,將會是無限多位,而且不會循環的小數。
圓周率不會循環,但是否可能有其他規律呢?雖然不排除這樣的可能性,但目前普遍認為圓周率是完全無法預測、完全沒有規律的,如果某天竟有人能從圓周率中發現某些規律,那肯定會震驚全世界。
●問題2╱如何寫進算式 數學家用π表示
小數和分數都無法確切地表現出圓周率,那麼問題來了,如果我們要把圓周率寫在算式中該怎麼辦呢?
從1647年起,開始有些數學家使用希臘字母「π」(讀做pi)表示圓周長或圓周率,但直到瑞士的大數學家歐拉,在他1736年出版的書中用π表示圓周率起,此用法才開始快速地流傳開來。
這邊順道提供一個π的實際運用案例:如果一個圓形的直徑長是10公尺,那麼圓周長就是10π公尺,而31.4公尺只是近似值,並非實際值。
最後、也是最重要的事,由於π的值約為3.1415926,所以我們可以在3月14日(圓周率節)的15點9分26秒吃一口美味的派,品嘗「π」的美好!
作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中
原文出自《好讀周報》640期