文/洪介興
●學新概念要理解 不厭其煩去思考
學習新概念時,絕對不能只記結果,而是要能夠理解推理過程。
譬如在學習正負數的加減法,學到5-(-3)時,有些同學可能會以背口訣或記憶的方式學習。記下「負負得正」的口訣,或是記住「減去負數」就是「加上正數」。
一開始不會發現這種學習方式有什麼問題,感覺這樣學得很快,題目馬上可以做得出來。但以後學到更深入的相關概念時就很容易轉不過來,因為打從一開始就沒有真正學會基礎!
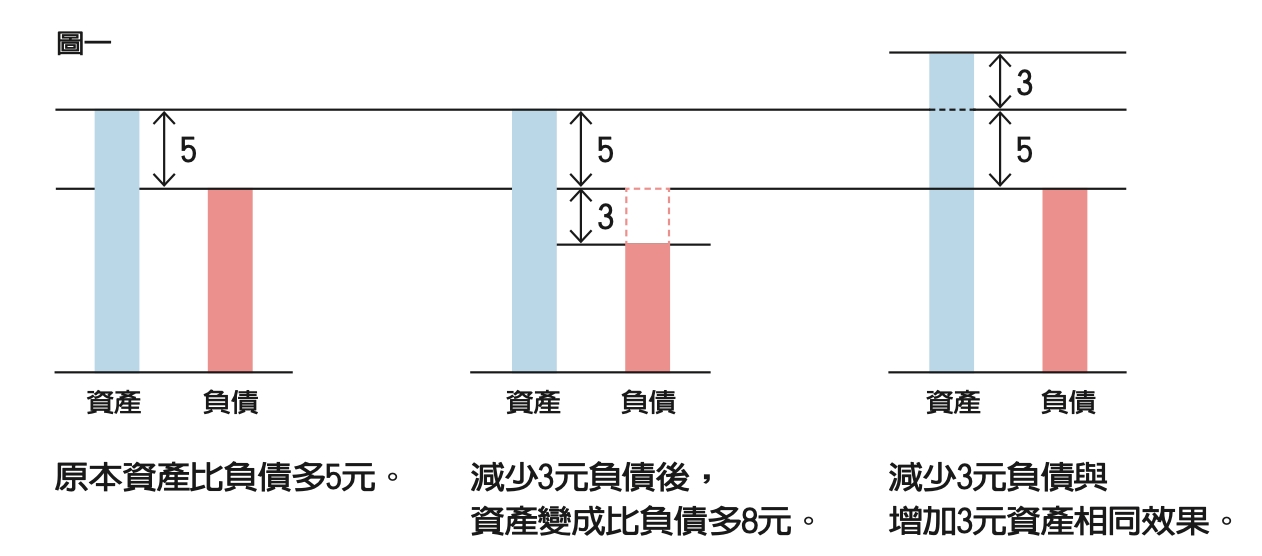
數學高手在學習時會積極去理解5-(-3)為什麼等於5+3,譬如他可能這樣想:把(-3)看成負債,那麼「減(-3)」就是「減少3元的負債」,這相當於資產增加了3元,所以5-(-3)就等於是5+3。(圖一)
不僅如此,在想通了減去負數會讓數值增加的道理後,數學高手也不會刻意記下這個結論,而是當下次又遇到類似狀況時,再重新想過一遍。
正因為不厭其煩地反覆思考,所以能把數學觀念學得很穩固,思考速度也越來越快。
●不侷限單一觀點 多元想法學更多
數學高手在看事情時不會侷限於單一觀點,而是會從各種不同角度來解讀一件事。以剛才的5-(-3)為例子,除了「減少負債」的想法以外,數學高手還會再用不同觀點來進行理解。
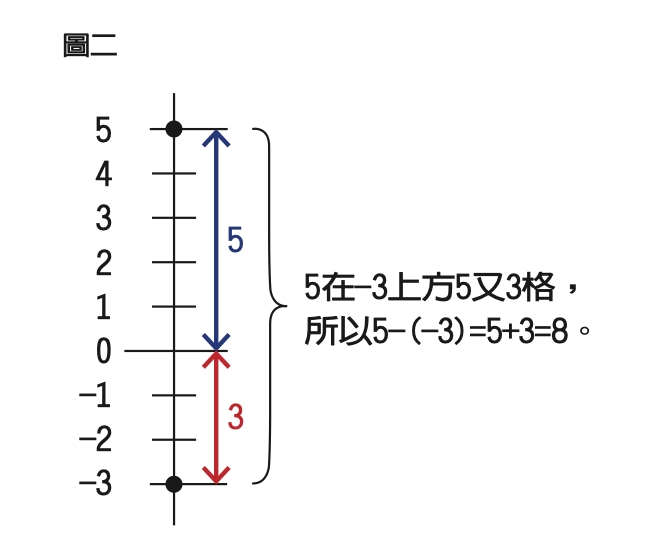
觀點二:減法一個很重要的功能就是用來計算「相差多少」,因此5-(-3)這個算式就是在看5和(-3)相差多少。因為5比0多出5,而0又比(-3)多出3,所以5總共比(-3)多出5+3,也就是說5-(-3)=5+3。(圖二)
觀點三:負數和正數的性質相反,當減去正數的時候,數值會變小;而當減去負數的時候,數值則會增加。所以「減去負3」會是「增加3」。
觀點四:加法和減法是相反的運算,當加上負數的時候,數值會變小;而當減去負數的時候,數值則會增加。所以「減去負3」會是「增加3」。
這些多元的觀點,讓數學高手對單一概念有更立體、更深刻地認識。一方面能讓這些數學概念在需要時更容易被喚起,並得以更適切地運作;另一方面還能讓不同數學知識產生連結,像上述的觀點二可以連結到高中數學會學到的「向量」概念,而觀點三、四提到反元素與逆運算也是很重要的數學觀念。因此各個數學概念不只是獨立的知識點,而是能形成一個脈絡完整的知識體系。
●讀題先想像情境 從中找重要數據
接下來我們以下面這道問題來示範數學高手是怎麼進行讀題的:
小明去公園慢跑,他繞著公園跑了三圈,前兩圈平均每分鐘跑180公尺,第三圈平均每分鐘跑150公尺,總共花了32分鐘,請問小明總共跑了多遠?
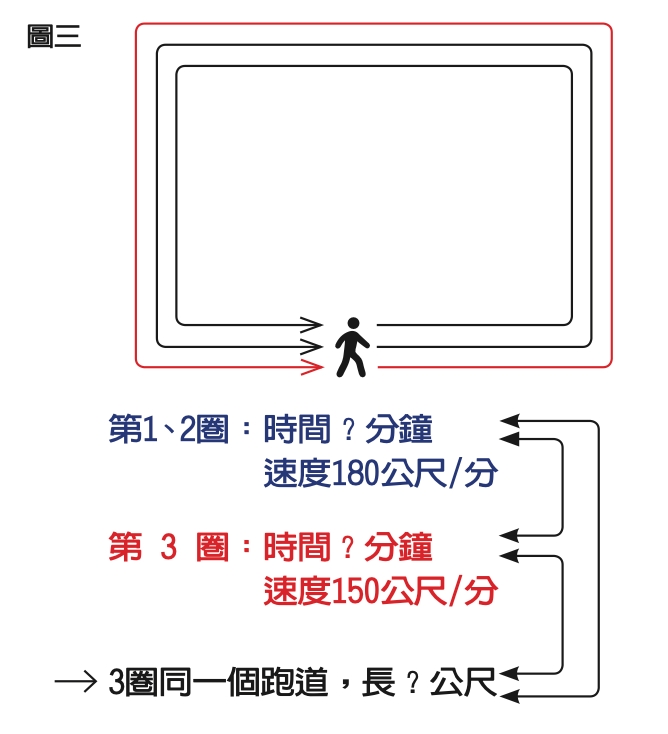
讀題時,數學高手會想像自己準備繞著公園跑三圈(圖三)。前兩圈的平均速率一樣,題目有告知前兩圈確切的平均速率,但沒有告知花的時間跟跑道長度;跑到第三圈慢了下來,題目一樣有告知明確的平均速率,但沒有告知花的時間跟跑道長度。另外題目有告知跑完三圈確切的總時間。
從上面的敘述我們可以知道,讀題時數學高手最在意的是故事中有什麼重要數據,以及題目有沒有提供這些數據的相關資料。先知道題目是直接告知確切的數值?還是告知數據間的關係?至於確切的數據是多少,只要知道題目有給就好,暫時不需要留意。
●要去理解數據關係 只背公式沒有幫助
讀題時也會把資訊做初步的處理,數學高手的思考如下:
題目雖然沒告知每一圈花費的時間和跑道長度,但有告知每一圈平均速率,所以只要有花費時間就可以推算跑道長度,也可反過來從跑道長度推算花費時間;或用「跑一圈的時間」乘以「平均速率」等於「跑道長度」的關係來列方程式。(圖三中的箭頭表示兩數量間有密切關連)
此外,題目還告知跑三圈的總時間,再加上知道第一、二圈花的時間相同,所以只要知道其中一圈的時間,就可推算另外兩圈的時間;或用「各圈時間相加」等於「跑三圈的總時間」來列式。
從「描繪情境」、「注意關鍵數據」到「初步處理資訊」就是數學高手在讀題時所做的工作。像這道題目是主角繞著公園一圈圈地跑,跑步通常會在意一圈跑多久、跑道多長,而這兩項數據正是這題的重要關鍵,所以將自身代入情境有助於我們注意到關鍵數據。
有些人會去背「速度×時間=距離」,但這種方式對學好數學是沒有幫助的。正確做法是想像出畫面,1分鐘前進180公尺,2分鐘就是2個180公尺,那麼幾分鐘就是180公尺的幾倍,所以跑一圈的時間乘以平均速率「當然」就是跑道一圈的長度。「當然」這兩個字很重要,表示我們非常瞭解這些數量間的關係,而不是刻意去記憶。
●先做整體構想 再來列式運算
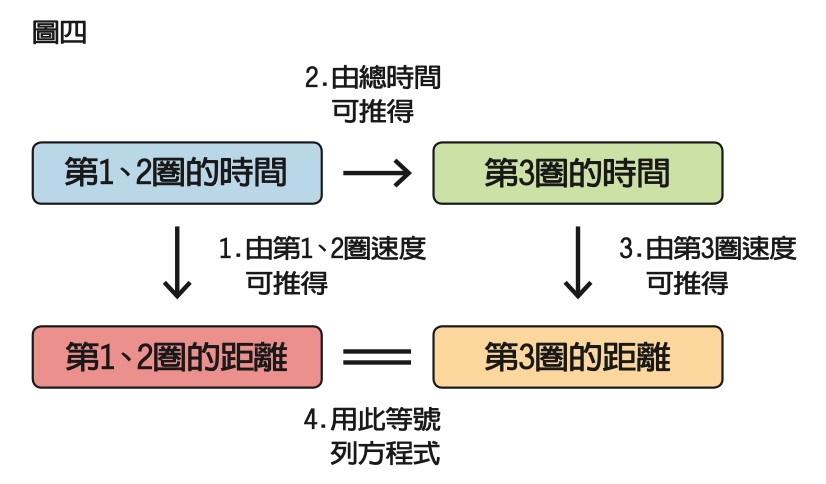
完成讀題後,下一步是對解題過程做出整體性的構想,先前讀題時注意的數量關係此時會發揮很大的作用。以前面的題目為例,可能會順著以下四個步驟進行構想(圖四):
①只要有第一、二圈花費的時間,就可以利用已知第一、二圈的平均速度推算出跑道長度。
②利用已知的總花費時間,可推算出第三圈花費的時間。
③有了第三圈花費的時間,再加上已知的第三圈平均速度,也可以推算出跑道長度。
④兩種不同方式都能推算出相同的跑道長度,因此只要把第一圈花費的時間假設為x分鐘,就可以把兩種不同推算跑道長度的方式列成一條等式。
先做好解題構想才進行列式、運算等解題工作,過程中才能條理分明而不至於迷失方向;當解題遭遇困難時,也更能適時而有效地調整解題策略。
●解完題要回顧歷程 多嘗試各種解題法
解題完成時,數學高手不會急著做下一道問題,而是馬上有重要的腦力工作要做。
首先要對剛經過的解題歷程進行回顧,看看這個解題方法與題目的關聯,想想這個解題方法為什麼可以解得了這道問題。經過回顧,可以把這一次的解題經驗更加精煉,未來如果有運用類似解題方法的機會,就更能夠適時適所地提取出來。
接著要再多試試其他解題方法,譬如剛才的題目也可以假設跑道長度為x公尺,分別推算出三圈花費的時間,利用三圈總和32分鐘來列出方程式。或是也可以利用第一、二圈和第三圈的速度比為6:6:5,距離相同下,得知花費的時間比為5:5:6(1/6:1/6:1/5);因此三圈花費的時間分別是10分鐘、10分鐘、12分鐘,如此立即就可以推算出跑道長度為1800公尺。
將幾個不同的解題方法進行比較,想看看為什麼有些方法在這道題目行不通?為什麼有些方法在這道題目比較有效?怎麼做可把這題的解題方法更加優化?有了這些深入的思考,對於這道數學問題的相關認識會更加全面,對諸多解題工具的了解也會更加深刻。
準備好成為數學高手了嗎?只要養成上述的思考習慣,你就是數學高手俱樂部的一員囉!
原文出自《好讀周報》752期

卷末,除了常見的地理要素,還記錄當時對海域的觀察。圖/故宮提供-300x203.jpg)

