文/洪介興
●考考你/0~2000抽20個數 最快時間答出平均數
現在請你準備好計時器,讓我們來玩一個小遊戲。下面的表中有20個數,是利用電腦程式隨機從0~2000中抽取出來的(抽取的規則是每個數被抽到的機率相等,抽過的數可以重複抽)。
請你計時並回答這20個數的平均數,並記錄下你回答所花的秒數,然後按以下規則計算你的分數,分數越低越好!
分數=誤差+時間
「誤差」是指玩家的答案和正確答案的差距,用其中較大的數減去較小的數計算而得。譬如玩家回答937,而正確答案是939,那麼誤差就是2。
「時間」以秒為單位,譬如玩家花了3分39秒,也就是219秒。把誤差2和秒數219相加,合計玩家的分數是221分。
在剛才的例子中,玩家的誤差雖然很小,但花的時間很多,所以如果想把分數壓低,或許可以從節省時間下手。請你先想想看有沒有什麼可以大幅節省時間的估算方法,再開始進行挑戰,找幾位朋友一起比賽會更加有趣喔!
請先把遊戲玩過後,再繼續接著把本文看下去吧。
●告訴你/四捨五入法 速度拖慢 無條件捨去 準確性差
一個很直覺的估算方式是只取到百位數做計算,然而這個想法很快地又會產生出兩個分歧的做法。一是四捨五入法、二是無條件捨去法,你覺得這兩種方法哪一種比較好呢?
若以準確性為考量點,四捨五入法肯定是比較好的方法,但相較於無條件捨去法,用四捨五入法會把速度拖慢非常多。
當使用無條件捨去法的時候,只需要看著前一、兩位數來計算總和,非常方便。但如果用四捨五入法,一來要多花一些心神判斷該進位還是捨去;二來若遇到進位時,要加的數並不是眼睛所看到的數,相當不直覺。多這兩層的處理,勢必會多花不少時間。
有沒有和無條件捨去法差不多快,又能讓誤差不要太大的方法呢?
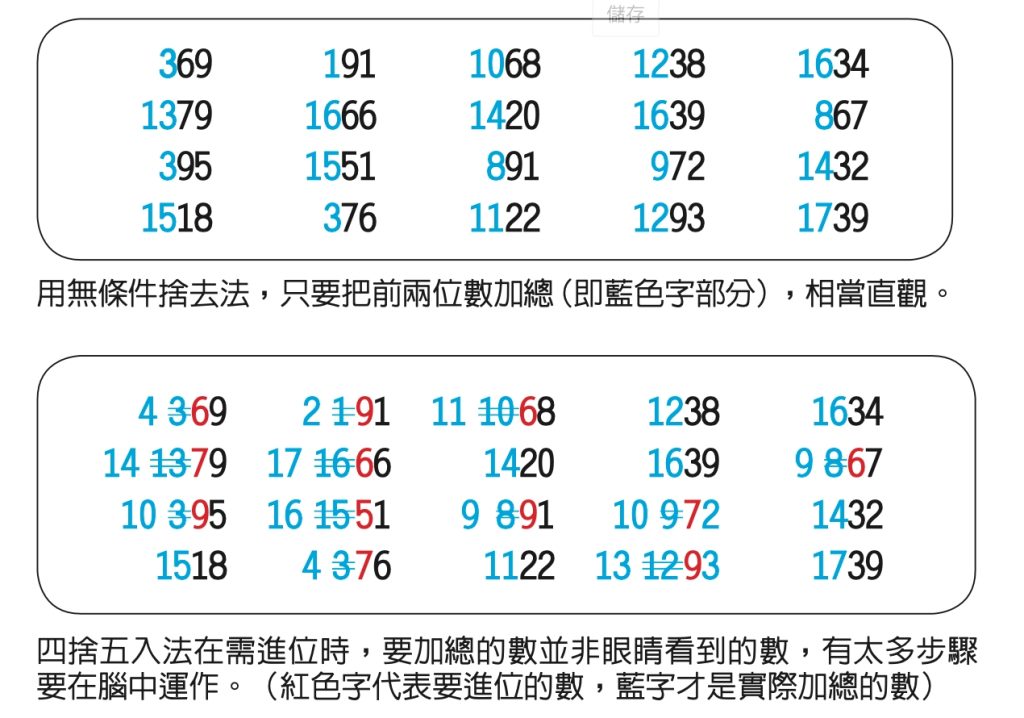
●有一招/前兩位 無條件捨去法相加 十位數 四捨五入法再調整
想想看四捨五入法跟無條件捨去法的差別,當十位數是4以下的數時,兩種方法要加的數是相同的;但當十位數是5以上時,用四捨五入法要加的數會比用無條件捨去法還多1。
經過以上的分析,不難想出一個和四捨五入法有相同效果,但更加有效率的方法。就是先用無條件捨去法的方式把前一、兩位數加好(總和是216)。完成後再來看所有的十位數,每看到一個要進位的數就再加1。加完的結果是228,因此最後計算平均數就是22800÷20=1140。
真實的平均數是1138,如果純粹用無條件捨去法,計算出的答案會是21600÷20=1080,誤差是58。但只要像剛才所說,稍微多花一點時間調整,就可以得到誤差只有2的估計值呢!
除了前面所述的方法以外,這邊再提供一個不同的想法。先用無條件捨去法進行估算,再把得出的1080加上50,直接用1130做為估計值。理由是被捨去的二位數,平均通常不會離50太遠。這個方法顯然比剛才的方法更快,雖然誤差通常會比四捨五入法稍微大一點,但也還能接受,不失為一個快速估計的好方法。

●很好用/善用分配律 比憑空想省腦力
做完了加法的速算後,接下來我們試著做一些乘除法。先從下面幾道問題開始熱身,請你不使用紙筆,正確算出下面幾道題目的答案。
① 58×9
② 753×5
③ 346×25
第①題如果你是在心中做直式乘法,你必須憑空想像出以下的畫面,然後把7和5加起來,發現要進位,所以百位數要變成5,當你處理到這邊的時候,個位數是多少大概已經忘了,整個過程應該相當費神吧!
如果你發現58非常接近60,若先用60×9,再減去多算的2×9,變成在心中做540-18,因為18這個數很小,所以這個算法對頭腦的負擔也會比較小。這個算法其實就是分配律的運用。
分配律:a×(b+c)=a×b+a×c
同樣是利用分配律,與其把58拆成60-2,不如把9拆成10-1來得更輕鬆;先算58×10,再扣掉58,也就是580-58。為什麼這樣會比540-18更輕鬆呢?第一個原因是540經過的思考比較多(要先把58當成60,再經過60×9的步驟),而580只是在58後面補0。第二個原因是紙上就寫著58,比憑空想還要省腦力。
這個方法在任何打9折的場合都很好用,遇到打9折時候想成是原價乘以0.9比較不好算,用原價扣掉10%會容易許多。像原價2880元打9折就是2880-288,大約2600元(只要知道約略數字就好,差8元不影響我們決定是否購買)。
學習加減法的時候,會跟小學生說3和7是好朋友,4和6是好朋友。那麼在做乘除法的時候,我們可以說5的好朋友是多少呢?
第②題要憑空想像乘法會比較吃力,因此我們請5的好朋友來相助,把753×5改成7530÷2。請你試著算算看,是不是更容易了呢?
第③題的概念也類似,要乘以25實在是太困難了,但如果是除以4就容易做了,因此346×25我們就改用34600÷4來處理。
●再一招/從左到右 做直式乘法 隨時喊停 估算不離譜
熱身完畢,接著要進入高強度的部分了,這裡不要求做出精確的答案,只要盡快給出估計值就好。現在請你不使用紙筆,估計856×687。
687很接近700,因此把687當成700來估計應該不錯,但856就很困擾了,當成900或800的誤差都很大,這時候該怎麼辦呢?
這邊介紹一個解決辦法:直接把856×687當成856×700來算。如果第一時間的反應是「856×7很難耶」,那大概是因為你習慣用直式乘法從右邊做到左邊。其實在估算的時候,最好從左邊開始算。
做856×700要先算8×7(56);接著加上5×7(35),其中35帶頭的3要對齊剛剛56結尾的6,加起來就是595;做到這裡如果你的頭腦還撐得住,就繼續加上6×7=42,其中42結尾的4要對齊剛才595結尾的5,得到5992;最後補上結尾的兩個0,得出856×700=599200。
從前面開始做的好處就是隨時可以喊停,得到一個不錯的估計值,你不妨也練習計算看看476859×6,如果你只乘到前兩位,得到47×6=282,那至少2820000也是個很好的估計值,距離真實答案2861154不會差太多。
●獨門祕招/善用%數 算得快又誤差小
最後分享筆者的獨門估計祕招,就用剛才的856×687當例子。
①把原題目當成800×700,得到560000。
②856比800多出了剛好7%,而687比700少了大約2%,把+7%和-2%相加,得到+5%。(這兩個誤差可以相加的說明請見附註)
③把560000調整+5%,大約+30000,得到的估計值就是590000。這題的實際值是588072,因此上述估計的誤差不到2000,還不賴吧!
再看一個例子,估計71583×28172。
①先把原題目當成70000×30000,7×3=21。
②71583比70000多出了大約2%,而28172比30000少了大約6%,把+2%和-6%相加,得到-4%。
③把21調整-4%(約0.8),得到20.2,最後在小數點後補上8位,得到的估計值就是2020000000。這題的實際值是2016636276,誤差不到千分之2,如果有仔細地調整成2016000000,誤差甚至只會有萬分之3!
誰說71583×28172只能有一種答案?一味追求著標準答案,是多麼地索然無味啊!只有多思考、善用我們接觸過的各種知識,才能產生出諸多專屬於你的獨到見解與想法,而這才是數學的趣味所在!
原文出自《好讀周報》748期




偕綠光劇團吳定謙領銜主演「轉生到異世界成為嘉慶君──發現我的祖先是詐騙集團!」。圖/台灣戲曲中心-291x300.jpg)