文／林志鴻
●一張紙 如何測厚度 一頭象 如何測質量
開始學習理化時，第一個部分就是要學習如何測量，先從長度的測量、面積、體積，再來是質量的測量，如何正確使用天平，然後就是把質量和體積的測量合起來應用，測出物體的密度。
在實驗室裡，對於身邊能拿到的物品，使用排水法來測量物體的體積、用天平來量出質量，應該都可以測量出來。但是要如何測量一張紙的厚度，或是一頭大象的質量，可能要有一點巧思。
要測出一張紙的厚度：我們可以取一百張相同的紙張，疊在一起之後，再測出一百張紙的厚度，接著除以100，就可以得到一張紙的厚度。
要測出大象的質量，可以把大象切成一塊一塊，用天平把每一小塊都測出來，然後加在一起就可以了……，不行，這樣太血腥了！我們可以用石頭來代替大象，只要能確定石頭和大象重量一樣，我們就可以量出每塊石頭的重量，間接算出大象重量。
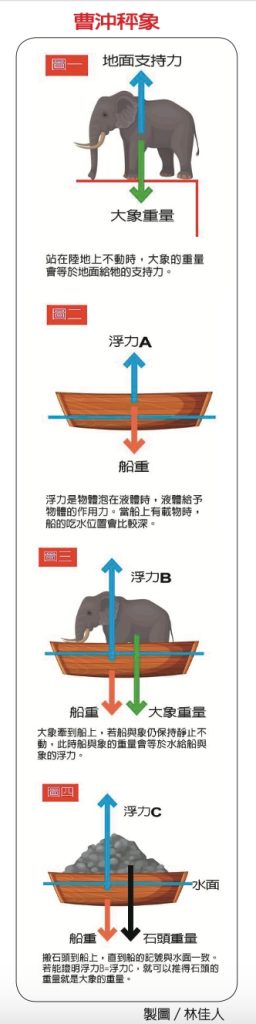
這招傳說是三國時代曹沖提出來的想法，如何確定石頭和大象一樣重？曹沖的方法是用船，把大象趕到船上，在船邊的水面位置作上記號，然後把大象牽下船，再用石頭一塊塊放入船中，讓船沉到剛剛作記號的地方，這樣大象就和石頭的重量一樣，再慢慢測出石頭的總重量即可。聽說當時曹沖才五、六歲左右，能想出這種方法，實在太厲害！
這個故事後來被人質疑大象的來源，當時的孫權不太可能養得起大象。這個故事的原型可能來自印度佛經《雜寶藏經》記載：「天神又問：此大白象有幾斤？而群臣共議，無能知者。……大臣問父，父言：置象船上，著大池中，畫水齊船，深淺幾許，即以此船量石著中，水沒齊畫，則知斤兩，即以此智以答天神。」故事可能以口語方式，輾轉流傳到中國，附會為曹沖秤象一事。
●萬有引力 牛頓提出定律 引力常數 卡文迪許算的
利用石頭來取代大象，就可以測出大象的質量！如果要測量地球的質量呢？難道要把地球切成一塊一塊，再把每一塊都量出來相加嗎？當然不是，要把地球質量測出來，需要介紹一位科學家：卡文迪許。
牛頓在1687年的《自然哲學的數學原理》提出萬有引力定律，但沒有把引力常數G給測量出來，這個數字非常小，大約經過一百年之後，1797年才由卡文迪許測出來。
要來自物理學家漢弗萊•戴維和其他一些朋友的記載，同時也流傳著不少傳說。據記載，卡文迪許長年穿著一件褪色的天鵝絨大衣，戴當時已經少見的三角帽，性格獨特，說話顯得猶豫和困難，而面對女士和陌生人會很羞澀而避免和他們說話。
他非常喜歡獨自沉思，甚至很少和自己的僕人見面，一般只會在桌子上留下字條說明自己晚餐要吃什麼，常常是「一隻羊腿」。
卡文迪許終生未婚，唯一的社會活動就是參加皇家學會俱樂部兩周一次的會議。他從不發表沒有研究透徹的東西，所以儘管他一生提交的論文不到20篇，卻獲得了皇家學會成員的一致尊重。
由於其家庭地位和父母留給他的大量財產，使得他曾是倫敦銀行的最大儲戶，但他心思專注在科學研究中，對於財產，他幾十年都只讓投資顧問買一種股票，不論漲跌。他的一名投資顧問建議他投資另一種股票，卡文迪許以平生罕見的大怒告知對方：「不要拿這些事情來煩我，否則我就解僱你」。故法國科學家必歐曾說「卡文迪許是有學問的人中最富有的，也很有可能是富有的人中最有學問的。」
1851年，由第一個發現色盲的化學家喬治‧威爾遜出版一部關於卡文迪許的傳記，書中對卡文迪許生活中各個方面的仔細觀察和描繪，被美國精神學院學者視為判定卡文迪許是一個亞斯伯格症候群患者的有力證據。
●只是測出引力常數 為何就知地球質量
卡文迪許測量引力常數的實驗設備是約翰‧米切爾設計，但米切爾本人不久去世，將裝置留給威廉‧海德‧沃拉斯頓，後被轉送給卡文迪許。
卡文迪許製造的實驗裝置是一台扭秤。用線捆綁的1.8m長的木棍兩端各有一個直徑2-英寸（51-公釐），重為1.61-英磅（0.73-公斤）的小鉛球。兩個直徑12-英寸（300-公釐），重為348-英磅（158-公斤）的大鉛球分別放在小球附近大約9-英寸（230公釐）遠，各自用懸掛裝置掛起。實驗即測量大球和小球之間微弱的重力。為了消除氣流干擾，卡文迪許將裝置安裝在不透風的房間，自己則在室外用望遠鏡觀測扭矩的變化。扭矩的微小轉動可由聚光光源射向鏡子反射到量尺上，只要扭矩轉動，就可以測出光點在量尺上的變化。
卡文迪許測得的數據換算成現代公認的引力常數 ，誤差不到1%，可謂是古典物理實驗中的經典實驗，值得讓學習普通物理的學生好好見識。
為什麼卡文迪許的實驗稱為測量地球質量的實驗呢？不是只測出引力常數G值的大小嗎？這跟地球質量有什麼關係呢？
我們取一質量為m的物體，在地表附近所受的重力為mg，如下圖左。
將此圖放大到如右圖，這個物體受到地球的萬有引力為卡文迪許測量引力常數的實驗設備是約翰‧米切爾設計，但米切爾本人不久去世，將裝置留給威廉‧海德‧沃拉斯頓，後被轉送給卡文迪許。
卡文迪許製造的實驗裝置是一台扭秤。用線捆綁的1.8m長的木棍兩端各有一個直徑2-英寸（51-公釐），重為1.61-英磅（0.73-公斤）的小鉛球。兩個直徑12-英寸（300-公釐），重為348-英磅（158-公斤）的大鉛球分別放在小球附近大約9-英寸（230公釐）遠，各自用懸掛裝置掛起。實驗即測量大球和小球之間微弱的重力。為了消除氣流干擾，卡文迪許將裝置安裝在不透風的房間，自己則在室外用望遠鏡觀測扭矩的變化。扭矩的微小轉動可由聚光光源射向鏡子反射到量尺上，只要扭矩轉動，就可以測出光點在量尺上的變化。
卡文迪許測得的數據換算成現代公認的引力常數 ，誤差不到1%，可謂是古典物理實驗中的經典實驗，值得讓學習普通物理的學生好好見識。
為什麼卡文迪許的實驗稱為測量地球質量的實驗呢？不是只測出引力常數G值的大小嗎？這跟地球質量有什麼關係呢？
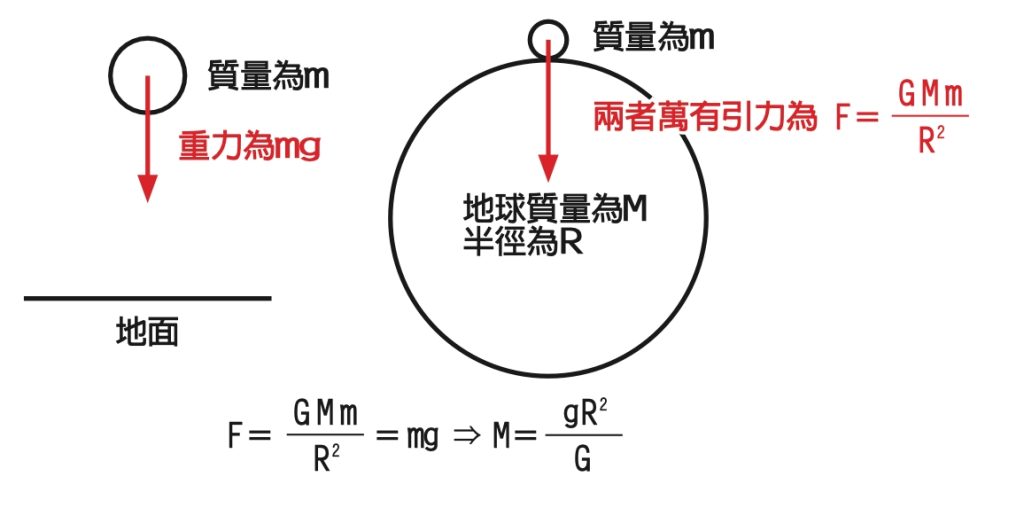
我們取一質量為m的物體，在地表附近所受的重力為mg，如下圖左。
將此圖放大到如右圖，這個物體受到地球的萬有引力為F＝ GMm／（R的平方）。
此兩力是相同的力。
如上所示，地球質量M就可以從上式求得：
g為重力加速度9.8m/（s的平方），R為地球半徑，G是卡文迪許測出的引力常數。
●地球半徑如何測出 利用陽光直射估算
一下，地球半徑是怎麼測出來的呢？其實，g、R、G這三個數字，最早被測出來的是地球的半徑，早在公元前240年就由古希臘的天文學家愛拉托斯特尼（Eratosthenes），利用陽光的直射估算出地球的半徑。
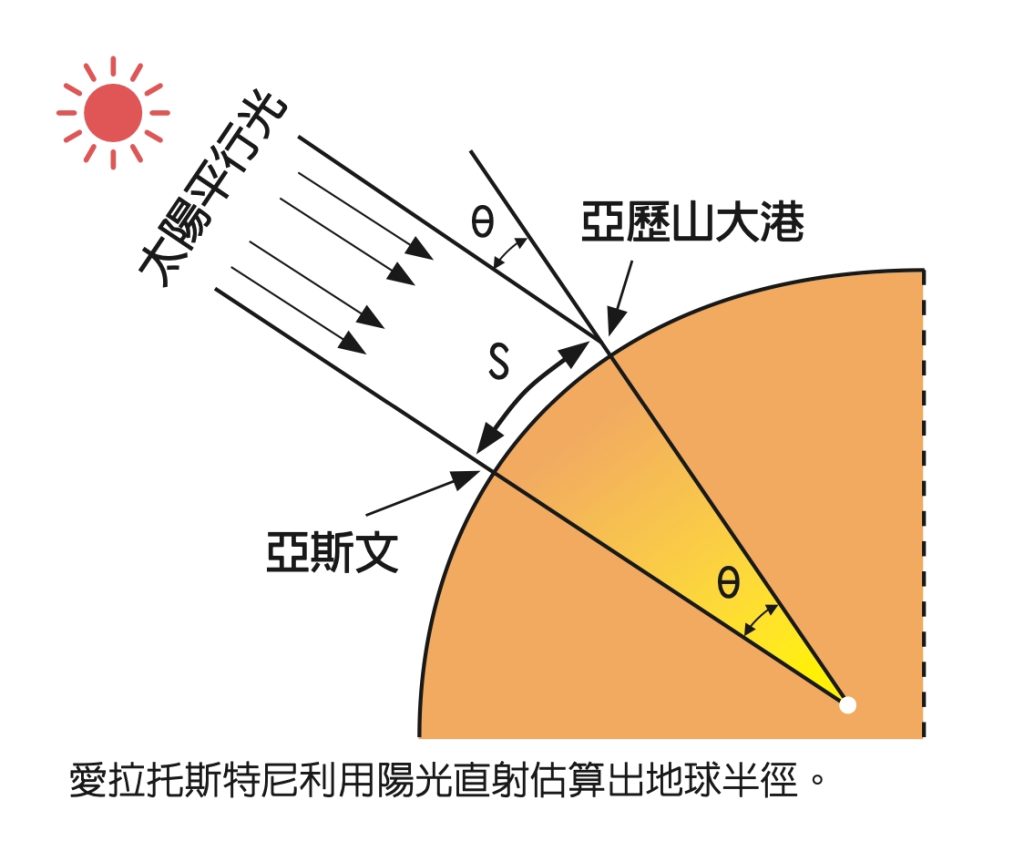
愛拉托斯特尼知道在一年之中白天最長的那天（夏至日）正午時分，太陽正好在亞斯文天頂的位置，因為此時太陽光直射入亞斯文城內的一口深井中，並在井底的水上反映出太陽的倒影。
他假設他的家鄉亞歷山大港在亞斯文的正北方（實際上亞歷山大港在亞斯文偏西一個經度）。他在夏至日正午時分，測量了亞歷山大城裡一個方尖石塔投下影子的長度，計算出了這個時候太陽在亞歷山大的天頂以南7°。他推斷出亞歷山大港到亞斯文的距離一定是整個地球圓周的7/360。
他從商隊那裡知道兩個城市間的實際距離大概是5000視距（stadia，又譯作「斯塔德」、「斯泰特」）。他最終確立了700視距為一度。從而得出地球圓周為252,000視距。
雖然視距的確切長度現時已無法考證（現在雅典的視距一般是指185公尺），但是現在普遍認為他推斷出的距離應該在39,690公里到46,620公里之間。（經過兩極的地球實際周長是40,008公里）
這種方法的關鍵在於同一時刻測量陽光的角度，這樣你就可以比較地球上不同地點的陽光入射角差異，並且使用三角學計算地球的半徑。愛拉托斯特尼當時使用這種方法精確地估算出了地球的大小，他的方法被視為古代地球測量的重要里程碑。
按現代公認的地球半徑R=6370.856公里，代入公式中，利用萬有引力來推算，可以得出宇宙中所有天體的質量，所以卡文迪許不只測得了地球的質量，還把所有天體的質量也「順便」測出來了！
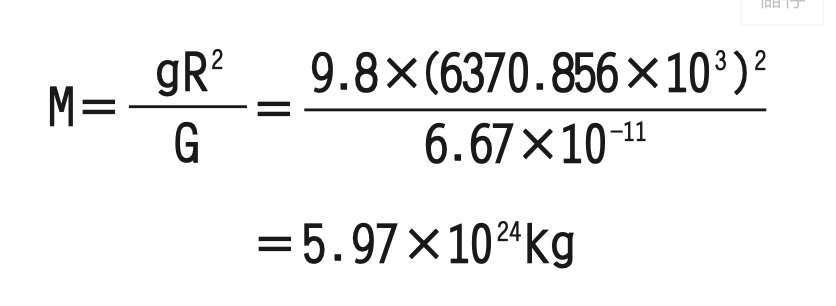
原文出自《好讀周報》745期
