文/洪介興
●古埃及/土地如何畫直角 利用長繩有撇步
古埃及是世界上最古老的人類文明之一,大約6000年前左右已在尼羅河中下游地區形成國家。
古埃及人將一年分為三個季節:11月到3月土壤濕潤、肥沃,是種植作物的季節;3月到7月是旱季,也是收成的季節;而7月到11月是尼羅河氾濫的季節,大洪水會將農地完全淹沒!
對古埃及人而言,尼羅河氾濫非但不是災禍,反倒是恩典!因為洪水帶來的腐植質、礦物質,讓土地更加肥沃,有利作物的生長。每年8月15日的「氾濫節」至今仍是埃及重要的傳統節日。
那麼問題來了,被河水淹沒過的土地,要重新畫分成一塊塊方正的田地。為了避免爭議,畫出來的直角一定要準確。我們雖然能用三角板輕易地在紙上畫出準確的直角,但三角板太小了,用來畫分土地一定會偏掉、會不準確,是不是要準備一個超大的三角板來解決這個問題呢?
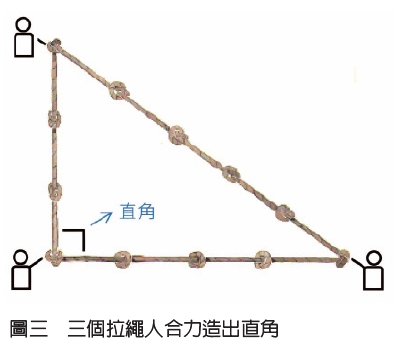
底比斯墓室群的壁畫(圖一)提供了一個重要線索,古埃及人會利用綁了繩結的長繩作為測量工具。另一個線索則是來自莎草紙(圖二)上的記載,古埃及人知道一個關於直角的重要知識:用3、4、5做為三個邊長,可以得到一個直角三角形!
結合以上兩個線索,我們可以推測,古埃及人很可能利用長繩來做出特大號的直角三角形。如圖三,只要準備長度12單位的繩子,由三個拉繩人遠遠地將繩子拉緊,只要三角形的三邊長度分別是3、4、5單位,就可以得到一個特大號的直角三角形了。
●巴比倫/出土泥板藏玄機 記錄「畢氏三元數」
知道三邊長為3、4、5可構成直角三角形。不只如此,在一塊出土的泥板(編號Si322)上,有著楔形文字記載的3組整數。除了前述的3、4、5以外,還有8、15、17,以及5、12、13,用這3組整數做為邊長都可以構成直角三角形。
更驚人的發現在P322泥板上,學者推測它的年代大約在西元前1800年左右,也就是距今約3900年前。這塊泥板上記錄了15組可構成直角三角形,其中最大的一組數是12709、13500、18541!
像這樣可構成直角三角形邊長的整數組合稱為「畢氏三元數」。古巴比倫人能發現這麼大的一組畢氏三元數,絕對不可能是透過經驗或測量。他們一定有掌握到如右圖的定理。
這個數學定理世稱「畢氏定理」,「畢氏」是古希臘數學家畢達哥拉斯(Pythagoras,西元前570~495年),他的出現比P322泥板晚了一千多年,可見寫下這塊泥板的古巴比倫人完全不知道這號人物,那麼為什麼這個定理會以畢達哥拉斯為名呢?

●古希臘/泰利斯加入驗證 幾何學成嚴密體系
研究圖形的知識稱為「幾何學」,英文是Geometry,源自古希臘文。geo是關於「土地」的字根,而metry是關於「測量」的字根,前後連起來就是「土地測量」,由此可見古希臘人把幾何學視為土地測量相關的學問。
尼羅河的氾濫不僅滋潤了大地,也促使古埃及人掌握大量的幾何學知識。大約在西元前600年左右,古希臘城邦米利都出現了一位智慧過人的商人泰利斯(Thales,西元前約624~546年),他到埃及、巴比倫從事商業貿易之餘,不斷充實知識與見聞,他在埃及待了很長的時間,向當地的祭司學習幾何學。
然而泰利斯並非只是單純地吸收知識,而是開始加入數學證明,逐一確保這些幾何知識的正確性。有了「證明」後,知識就不再只是零散的事實,而是能形成一個完整而嚴密的體系。泰利斯做學問的方式帶給西方科學深遠的影響,故而被後世頌為「科學與哲學之父」,也稱「數學之父」。
幾十年後,在薩摩斯島又出現一位大學者,他就是畢達哥拉斯。畢達哥拉斯也曾至埃及和巴比倫遊歷、累積知識,並曾向泰利斯學習。他同樣以嚴謹的邏輯方法進行數學研究,並有許多追隨者,形成極具宗教神秘色彩的學派,在數學、科學、哲學、音樂、美學等諸多領域都有相當大的成就。
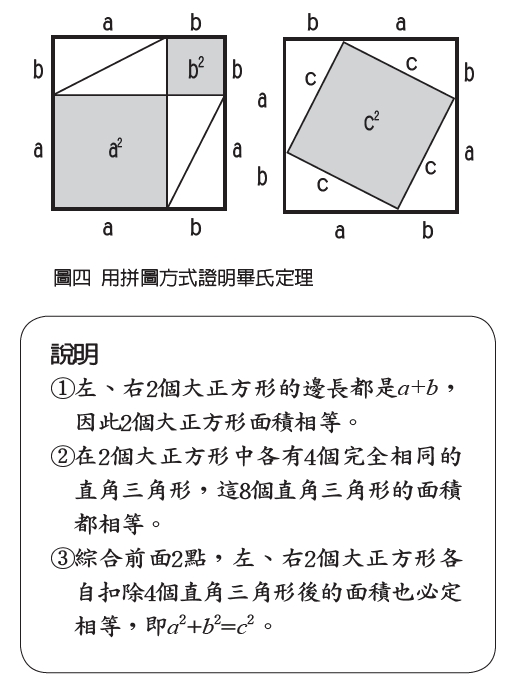
相傳畢達哥拉斯是史上第一個證明畢氏定理的人,因此畢氏定理(Pythagorean theorem)便以他為名,可惜至今查無相關文獻,因此畢氏定理是否由畢達哥拉斯或畢氏學派證明出來,以及證明的方法都不得而知。下面提供一個拼圖的證明方法,稍微彌補一下這個缺憾。(見圖四)
●古中國/《周髀算經》有記載 三國趙爽發揚光大
來到古中國,畢氏定理叫做「勾股定理」或「商高定理」。此定理會稱作勾股定理,是因為在《周髀算經》中,勾表示直角旁較短的一邊、股表示直角旁較長的一邊。而《周髀算經》記載到勾股定理的地方,其實是西周初年的數學家商高,大約在西元前1000年左右與周公的一段對話,因此又叫作商高定理,這是勾股定理在古中國最早的文字記載。
「故折矩,以為句廣三,股脩四,徑隅五。既方之外,半其一矩。環而共盤,得成三、四、五。兩矩共長二十有五,是謂積矩。故禹之所以治天下者,此數之所生也。」
這段話提到大禹做工程時就用到這個數學性質,和古埃及人的做法一樣!同時這句話還隱含一個意義,就是早在商高之前的專業人士就知曉此性質。
《周髀算經》的原文只能解釋3、4、5這個特例,而三國時期的吳國數學家趙爽在為《周髀算經》做註解時(約西元222年),根據原文畫出了圖五,並進行較為詳細的說明。趙爽的說明可適用於任意的直角三角形,在古中國的文獻中,這是首度對畢氏定理有一般性的證明。趙爽用「中黃實」加上4個「朱實」來計算斜邊為邊長的正方形面積,以現代的數學式說明如圖,這會用到些許八上數學第一章的知識。
畢氏定理是幾何學最重要的基石,本文僅和讀者一同初步認識這個數學瑰寶。與此定理相關的故事,以及有趣的數學知識多得不勝枚舉,等著我們大家繼續慢慢欣賞、細細品味喔!
原文出自《好讀周報》744期