Blog

【文╱洪介興】

●問問你╱明明是一條線 為何叫做圖形

有一次，一位學生這樣跟我說：「把二元一次方程式的圖形叫做『圖形』，結果卻只是一條直線，這樣未免也太空虛了吧！」說得真好，直線就直線，何必故弄玄虛地特別把它叫做圖形呢？

有些東西我們在剛開始學的時候會覺得怪，通常是因為我們還學得太少了。當學過的內容愈來愈多，逐漸形成體系時，很多疑惑便會煙消雲散。因此，我們現在要先來偷看一些高中才會學到的內容。

首先我們來看一個有點複雜的方程式：

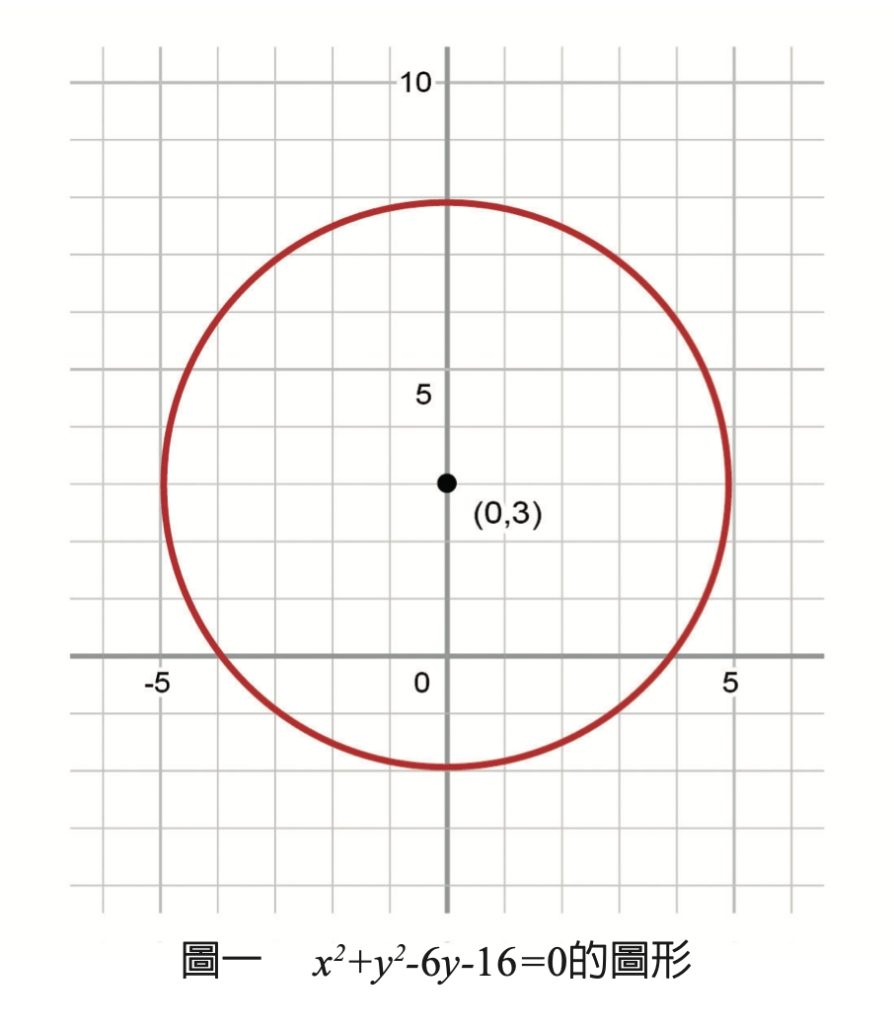
（x的平方）+（y的平方）-6y-16=0

發揮你的想像力，猜猜看這個方程式的圖形是什麼形狀吧！

答案揭曉，這個方程式的圖形是一個圓形！把它畫在平面直角坐標上，就是一個圓心在(0,3)、而半徑是5的圓形（如圖一）。你不妨找幾個圖形上的點，譬如像是(4,0)、(5,3)、(0,8)等，將它們x、y坐標的值代入方程式檢查看看。此外，這邊有一點要注意的是，「圓形」指的是圓周部分，不包括內部喔！

●告訴你╱二元二次方程式 圖形主要有三類

剛才討論的（x的平方）+（y的平方）-6y-16=0是一個二元二次方程式，其圖形為圓形，但並非所有二元二次方程式的圖形都是圓形，事實上，二元二次方程式的圖形主要可以分為橢圓（圓形也包含在這一類）、拋物線、雙曲線這三類：

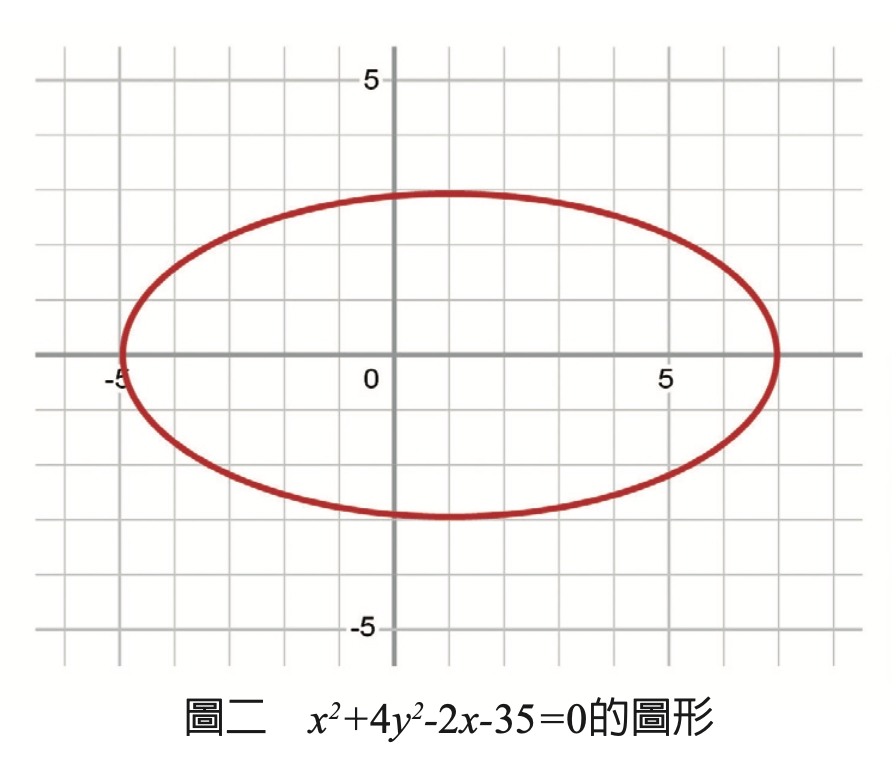
圖二是(x的平方)+4(y的平方)-2x-35=0的圖形，它是橢圓；

圖三是(x的平方)+4y-16=0的圖形，它是拋物線；

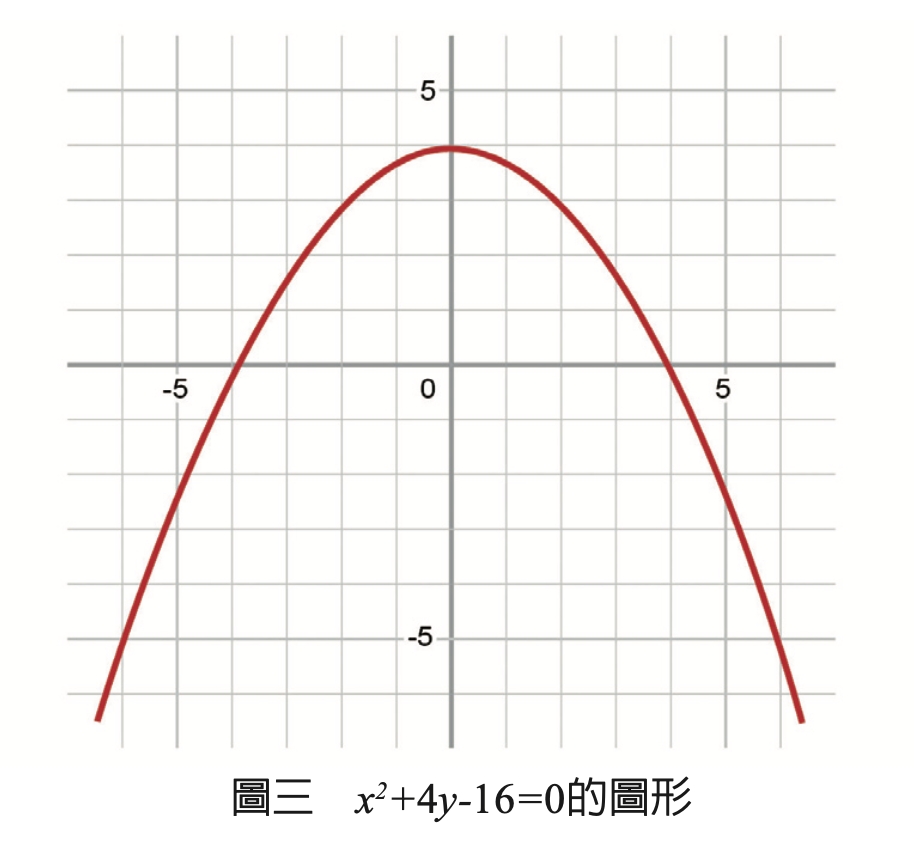
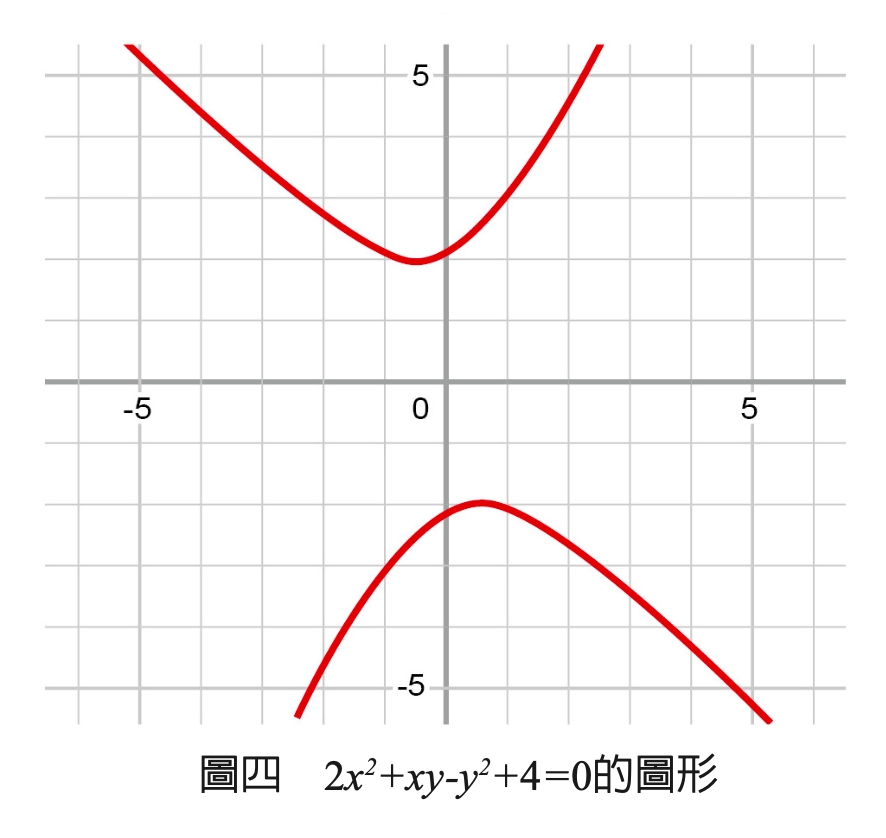
圖四是2(x的平方)+xy-(y的平方)+4=0的圖形，它是雙曲線。

●再問你╱方程式和圖形 結合有何意義

看到這裡你可能會想問，說了這麼一大堆彎彎圓圓、且我們不太熟悉的圖形，那麼怎樣的方程式圖形才會是三角形、四邊形等，這些我們比較熟悉的圖形呢？回答以後你一定會覺得：「啊！原來就只是這樣喔！」這邊先給你一個提示吧：三角形是什麼東西圍成的呢？

想到了嗎？只要用方程式畫出三條直線，不就構成一個三角形了嗎？

現在我們已經知道各式各樣的圖形如何跟方程式聯繫，但還有一個更本質的問題沒有解決，就是把方程式和圖形結合起來有什麼意義？為什麼要把方程式和圖形做結合呢？

●找關鍵╱學幾何沒有撇步？ 笛卡兒找到捷徑！

歐洲文明、乃至於現今主宰著全世界的科學，都可以說萌芽自古希臘。當時出現了許多偉大的文學家、史學家、藝術家、科學家、哲學家……，他們貢獻了極大的文化成就，為一千多年後的文藝復興、啟蒙運動、工業革命奠下基礎。

「希臘三哲」之一的偉大哲學家柏拉圖在西元前4世紀創立了「學院」，又稱「柏拉圖學院」，眾多學者在學院研究著各種學問，可以說是大學的前身。相傳在學院門口寫著這樣的標語──「不懂幾何學者，不得進入此門。」幾何學是研究圖形的學問，是數學的一個重要分支。前面這段話意謂著，對於古希臘的哲學家們而言，懂不懂幾何學是衡量一個人是否具備良好的邏輯思維能力的最佳標準。

承襲古希臘文化的托勒密王國也有相關的有趣故事。開國君王托勒密一世非常重視學術，他在亞歷山卓城建立了亞歷山卓博學院和亞歷山卓圖書館，吸引諸多學者在此研究各種學問，使亞歷山卓成為希臘化時代的學術、文化中心。相傳托勒密一世曾向大數學家歐幾里德學習幾何學，然而幾何學不僅邏輯嚴密，還常需要巧思奇想，且同樣的證明技巧放在別的問題往往無法適用，因此學習過程有時會有點辛苦。於是托勒密一世忍不住詢問有沒有學習幾何學的捷徑，歐幾里德的回答是：「沒有通往幾何學的皇家道路。」

然而，歐幾里德不知道的是，兩千年後，法國數學家（亦為哲學家、科學家）笛卡兒竟然找到了一條通往幾何學的高速公路！聰明的讀者，你能猜到這條捷徑是什麼嗎？

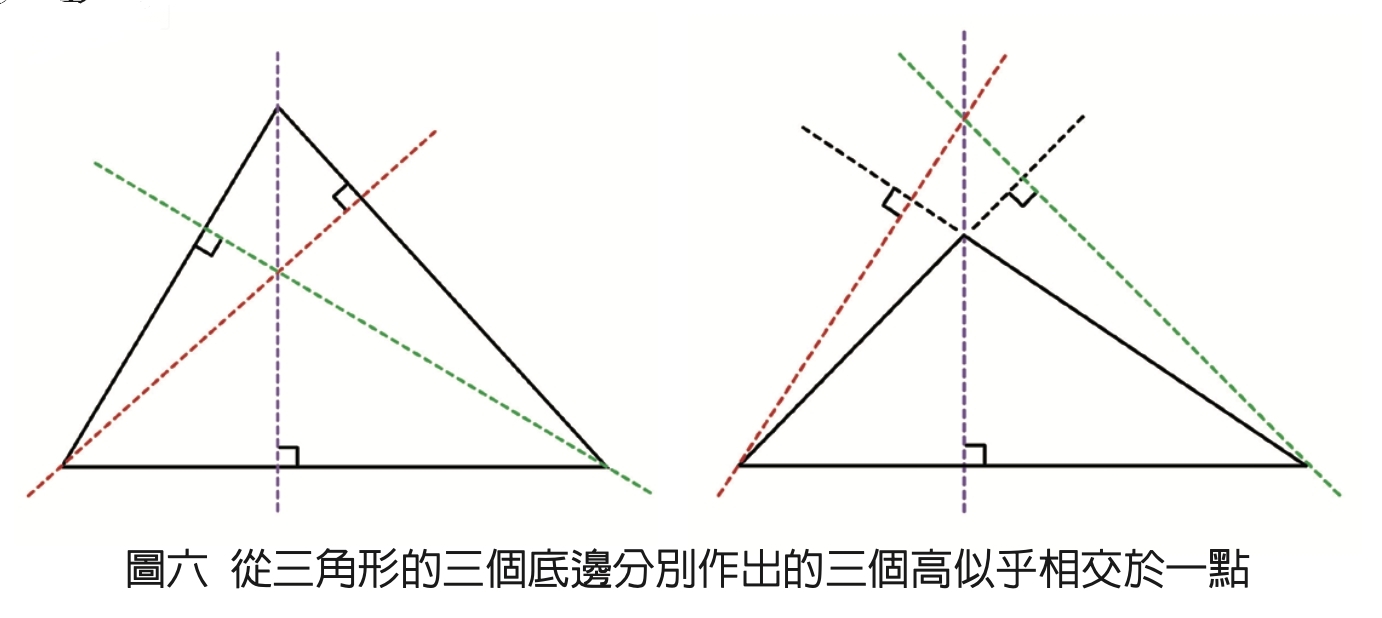
●看困難╱一個幾何證明 需要許多巧思

我們都知道一個三角形有三個邊，任意選其中一邊當作底邊，都可以畫一條相對應的高（如圖六）。有趣的是，三角形中的三個高似乎會相交於一點。會不會其實三個高沒有相交於一點，而是有一點點差距？會不會只有某些三角形的三個高會相交於一點？還是任意三角形的三個高都必定會相交於一點？這必須要靠嚴謹的數學證明才能證實。

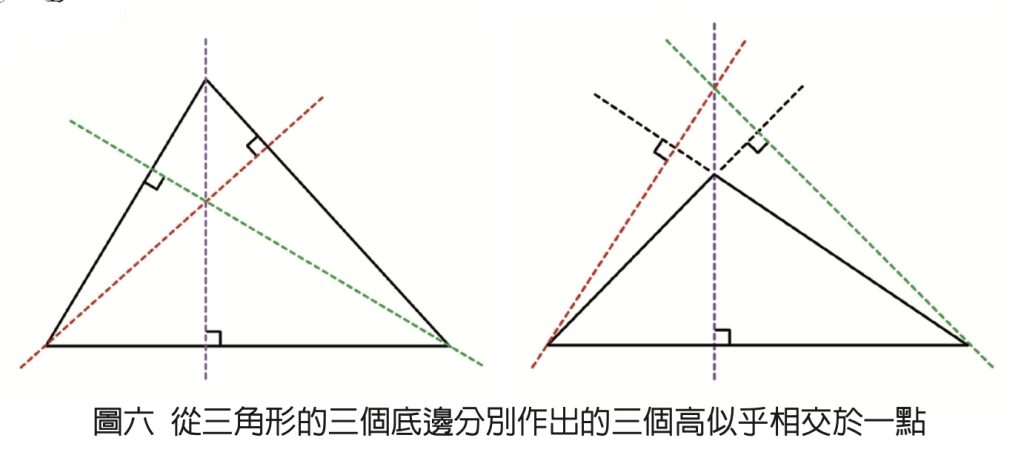
這邊我先直接講結論：任意三角形的三個高都必定會相交於一點。下面會將整個證明流程簡單扼要地呈現出來，其中會用到一些九年級才會學到的數學知識。無法完全看懂證明過程不要緊，這裡只是要讓讀者們瞭解，完成一個幾何證明往往需要許多巧思。

①如圖七，AD是BC邊上的高，BE是AC邊上的高，且AD和BE相交於點H。

②連接CH，與AB相交於點F，最終目標是要證明CF也是AB邊上的高。

③連接DE。

④因為點A、B、D、E在同一個圓上，所以∠BAD＝∠BED。

⑤因為點H、D、C、E在同一個圓上，所以∠HED＝∠HCD。

⑥由△ABD可看出一個紅色角和綠色角共90度。

⑦由△BCF可看出∠BFC＝90度，因此CF也是AB邊上的高。

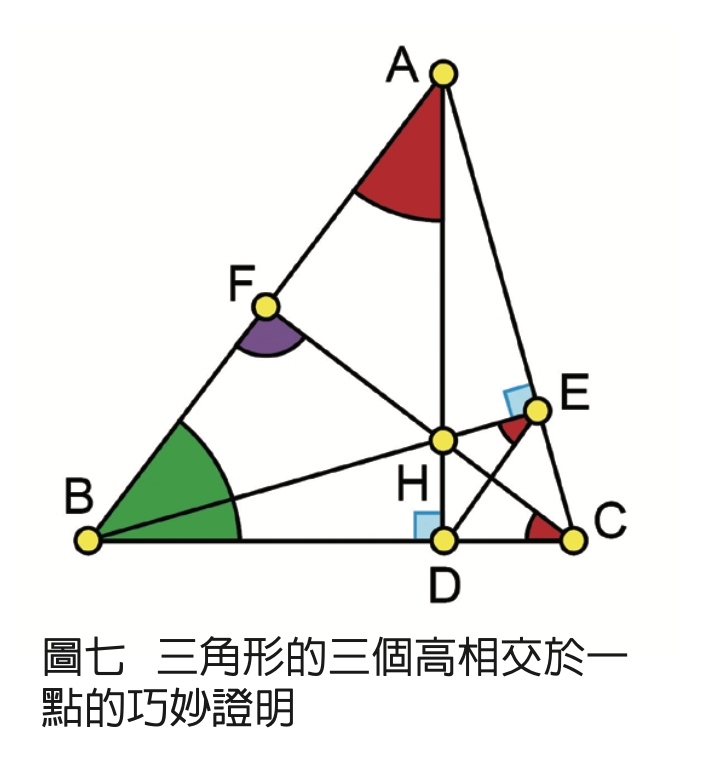
以上的證明運用了構造問題的技巧、四點共圓的想法、適當的輔助線、圓周角的性質、以及三角形內角和的性質。這些想法和幾何性質，單獨拆開來看都不難，但幾何研究的困難在於不容易想到證明的路線，只能憑藉一次又一次、一個又一個的巧思！

●有解方╱圖形結合方程式 幾何問題變代數問題

笛卡兒創立了解析幾何，透過圖形與方程式的結合，把幾何問題轉換為代數問題。原本需要許多巧思才能解決的幾何問題，變成只要會解方程式就能解開的代數問題，接下來便以相同的證明題──「證明任意三角形的三個高相交於一點」為例進行說明（如圖八）。

①假設三角形的三個頂點及其坐標分別是是A(0,0)、B(1,0)、C(a,b)。

②邊上的高，直線L的方程式是x=a，

邊上的高，直線M的方程式y=-(a-1/b) x ，

邊上的高，直線N的方程式是y=-a/b(x-1) 。

③將x=a分別代入另外兩條方程式，會得到相同的y值，表示直線L、M的交點和直線L、N的交點是同一點，也就是說三個高相交於一點。

有了解析幾何以後，許多幾何學的難題突然都變得十分容易。只要把圖形轉換為方程式，後續透過代數運算的技巧就可以輕易地解決問題，不需要特別的巧思。像上面的例子，只要熟悉把直線轉換成方程式的方法就能輕鬆解題，笛卡兒確實開創了幾何學的王者之道啊！

解析幾何雖然已經非常厲害，但圖形和方程式結合的重要性可是遠不僅於此！可惜礙於篇幅，今天我們就先談到這吧！

【2023-06-12/聯合報/R07版/好讀周報動腦力】