樣本分配沒你想像的平均
【文╱洪介興】 作者為教育部適性教學計畫「數學建築活動」教案設計人,任教北市石牌國中
●跟你同一天生日 30人中只有7.65%
你有沒有認識和你同一天生日的朋友呢?想想看,一年有365天,兩個人要湊巧在同一天生日,那可是相當不容易的一件事啊!
那麼,你是否曾遇過班上有兩個人同一天生日的經驗呢?
因為一年有365天,而一個班級大約只有20~30人左右,所以要有兩個人同一天生日應該還是非常困難才對,發生的機率應該不到10%吧!
以上這個想法看似合理,實際上卻是往錯誤的方向思考問題,因為題目問的是「有兩個人同一天生日的機率」,而不是「有人跟你同一天生日的機率」。
如果題目問有人跟你同一天生日的機率,那麼這個機率確實是不到10%,大約是百分之7.65,很接近13分之1。
這個機率是怎麼算出來的呢?先說結論吧,這個機率的計算方式是用1,去減掉365分之364的29次方;前面的「1」是全部的機率,而後者是全班沒有人和你同一天生日的機率,因此兩項相減就是有人和你同一天生日的機率。


●與其計算同一天生日 不如減去不同天生日
為什麼是這樣計算呢?這邊先用一個比較好懂的例子說明:
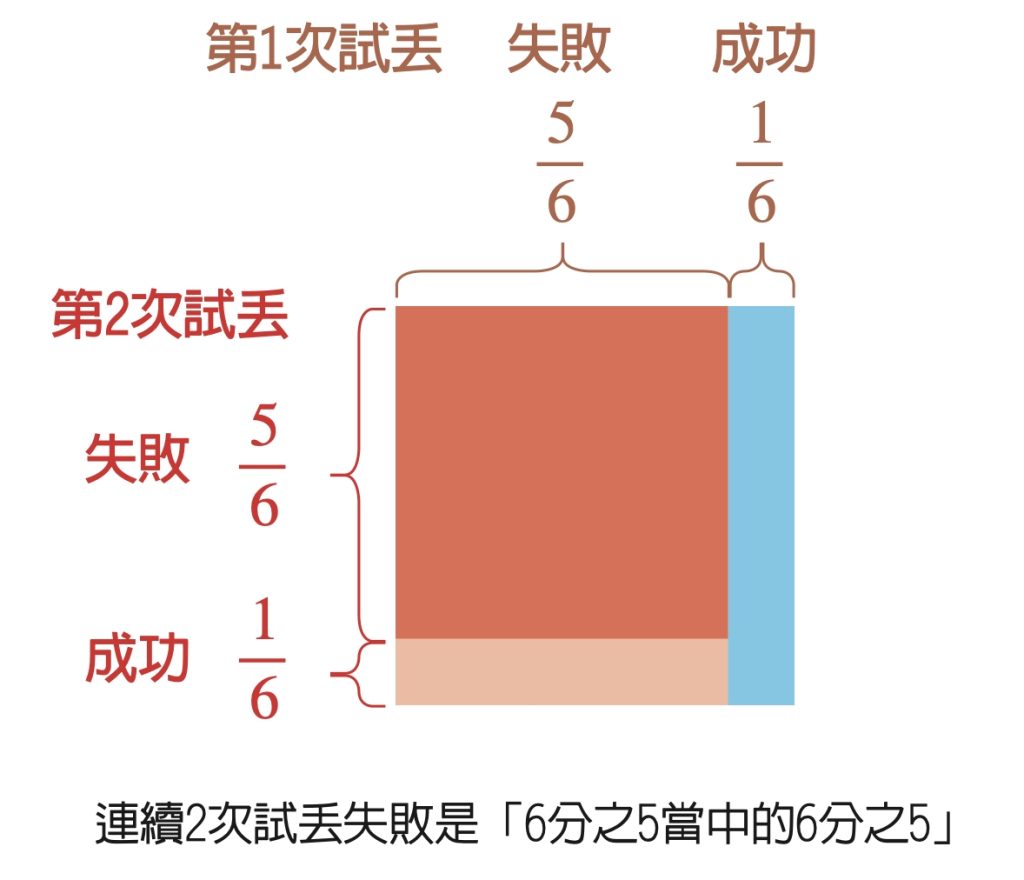
假設你現在丟一個公正的骰子,目標是丟出1。如果只能丟1次,那麼成功率就是6分之1,而失敗的機率是6分之5。
如果有2次試丟機會,成功率就是第1次試丟便成功的機率(6分之1),再加上第2次試丟才成功的機率;但第2次試丟才成功的機率怎麼算呢?其實要用第1次試丟失敗的機率(6分之5)去乘上第2次試丟的單次成功率6分之1,這是因為「第2次試丟才成功」要建立在「第1次試丟失敗」的前提上,所以是「6分之5當中的6分之1」,也就是「6分之5乘以6分之1」,即36分之5;把這個機率再加上第1次試丟的成功率(6分之1)後,便可得到2次試丟以內成功的機率(36分之11)。
如果有3次試丟機會,就要再加上前2次試丟都失敗,而第3次試丟成功的機率,這個情形是「6分之5當中的6分之5當中的6分之1」,也就是「6分之5乘以6分之5乘以6分之1」,即216分之25;再加上2次試丟以內成功的機率(36分之11)後,便得到3次試丟以內成功的機率為216分之91。
如果有4次試丟機會……,慢著,難道沒有更有效率的方法嗎?
有的,就是直接計算4次都失敗的機率,連續失敗4次就是「6分之5當中的6分之5當中的6分之5當中的6分之5」,也就是「6分之5的4次方」,即1296分之625;而1減去1296分之625剩下的1296分之671,就是4次試丟以內成功的機率囉!
回到生日的例子,全班30人當中有人跟你同一天生日的機率,就是用1減去29個同學都跟你不同天生日的機率,講解到這邊,你應該就可以明白前面的算式是怎麼列出來的吧!
●30人中有同天生日 機率竟然超過70%
現在我們再回到30位同學是否容易有人同一天生日的討論,為了有助思考,我們可以想成班上的同學是一個、一個地「降臨」班上的,就如同前面丟骰子的例子,是一次、一次地試丟一樣。
雖然我們想要知道的是有人同一天生日的機率,但其實在這個例子中,沒有人同一天生日的機率還是比較好算,以下我們就來練習計算沒有人同一天生日的機率。
①第1位同學降臨,沒有人同一天生日的機率是1。
②第2位同學降臨,他跟第1位同學同一天生日的機率是365分之1,因此沒有人同一天生日的機率是365分之364。
③第3位同學降臨,在前2位同學不同天生日的前提下,他跟前2位同學同一天生日的機率是365分之2,因此沒有人同一天生日的機率是「365分之364當中的365分之363」,也就是「365分之364乘以365分之363」。
④第4位同學降臨,在前3位同學不同天生日的前提下,他跟前3位同學同一天生日的機率是365分之3,因此沒有人同一天生日的機率是「365分之364當中的365分之363當中的365分之362」,也就是「365分之364乘以365分之363乘以365分之362」。
依此類推,30位同學都不同天生日的機率就是「365分之364乘以365分之363乘以365分之362……乘以365分之336」;再用1減去以上的計算結果,就得到有人同一天生日的機率,結果這個機率竟然超過70%,表示30人的班級有人同一天生日非但不足為奇,反倒是稀鬆平常的情形,30個同學都沒有人同一天生日反而還比較少見呢!
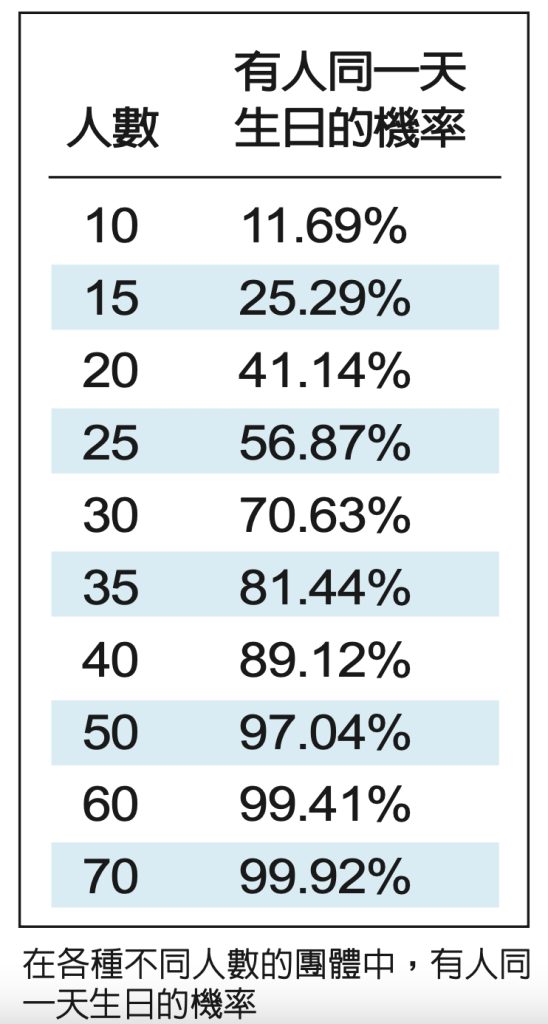
●天天有人過生日 2972人才90%機率
機率的觀念有個很常見的謬誤,就是人們往往會把樣本的分布想得過於平均。譬如剛才的例子中,人們容易認為大家的生日會散開在不同日子,而低估了有人同一天生日的機率;接下來我們也將繼續探討這個謬誤。
我在Facebook上有730多位朋友,正好稍微比365的2倍多一點點,有時候一天會有3、4個朋友的生日通知。這讓我想到一個問題:如果每位朋友都公開他的生日,我平均每天會有2個朋友過生日,會不會我其實已經蒐集到一年365天所有不同生日的朋友了呢?這樣的可能性大嗎?
事實上,根據詳細計算的結果,730個人的生日要分散到全年365天的機率可以說是微乎其微,就算把人數乘以2倍,1460人的生日大約也只有萬分之9.3的機率可以湊齊365天;若只有1350人,機率就只剩下萬分之0.7,更別提只有730個人的情況了。
當朋友人數到達1606人時,就會有百分之1的機率湊齊365天生日;而要1854個朋友才有10%的機會可以湊齊365天;若要有50%的機會,得要有2287個朋友才夠;想要十拿九穩的話,則需要2972個朋友,這樣才能有90%的機會湊齊365天的生日。
●全套10款抽幾次湊足 平均要抽29次才成功
你玩過扭蛋嗎?不同扭蛋機裡充滿著各式各樣可愛的小玩具,同一台機器裡通常是一系列6至10多種不同的小玩具,有些人沉迷其中,執著於蒐集全套公仔,殊不知這件事就像蒐集全年不同生日的朋友一樣,沒有想像中簡單。
以全套10款玩具為例,玩家可能以為抽個十幾顆應該就能湊齊一套,但事實上,平均要抽29次才能成功蒐集全套10款;如果全套有20種款式,蒐集全套平均更是需要抽71次才能成功,這個數字甚至都已經高於20的3.5倍了!
近幾年來,手機、電腦上充斥許多靠著扭蛋機制來營利的遊戲,讀過這篇文章的你,現在已經知道蒐集虛擬寶物並非想像中容易,在面對這類遊戲的誘惑時,一定要小心看好錢包、謹慎以對,別被一時的好勝心沖昏頭了!
【2022-10-31/聯合報/R07版/好讀周報動腦力】




