文╱曾慶良(阿亮老師)
●告訴你╱一維與二維條碼 商品碼分這兩類
我們每天在商店或者賣場消費時,店員都會拿著掃描機掃描產品包裝上的商品碼,以記錄購買商品所對應的金額,你有沒有很好奇怎麼不到一會兒的功夫就完成了結帳程序?今天我們就來看看商品碼的祕密吧!
目前市面上通用的商品碼大多有兩類,分別為一維條碼(Bar Code)和二維條碼(QR Code),一維條碼是以「數字編號」資訊來顯示編號識別商品,而二維條碼除了數字資訊外還可以顯示英文字母、中文等,可以容納7089個字元(常用的一維條碼則有13個字元)。
我們常看到的一維條碼是以一條一條黑色和白色條紋所構成,用掃描機掃碼若遇到黑色為不透光顯示二進位數字為1、白色則透光顯示二進位數字為0,條碼的左右被兩條最長的黑色條紋所匡列(稱為起始與終止字元),正中間兩條最長的黑色條紋則是用來區隔左右(稱為校正字元),而在起始與終止字元間則有:國家代碼、廠商代碼、產品號碼和檢核碼四個區塊(台灣的國家代碼為471);校正字元左邊的編碼規則可以用TypeA或TypeB,而右邊的編碼規則則需要使用TypeC;為了防止掃瞄條碼時誤判商品,所以會加上一位數的檢核碼。
●要知道╱檢核碼如何產生? 有固定的計算方式
檢核碼是依固定的計算方式求得。我們以471123456789為例,其計算規則步驟如下:
步驟①:將偶數位數相加後答案乘以3,此題為(7+1+3+5+7+9)×3=96
步驟②:將奇數位數相加,此題為(4+1+2+4+6+8)=25
步驟③:將前兩項數值相加後答案取個位數字,此題為96+25=121,則取個位數字1
步驟④:步驟③得到的數字若為0則檢核碼即為0,若不是0則以10減去,該數即為檢核碼,此題為10-1=9
目前許多的號碼(例如身分證、ISBN書籍編碼等)都有一套專屬的數學運算檢核規則。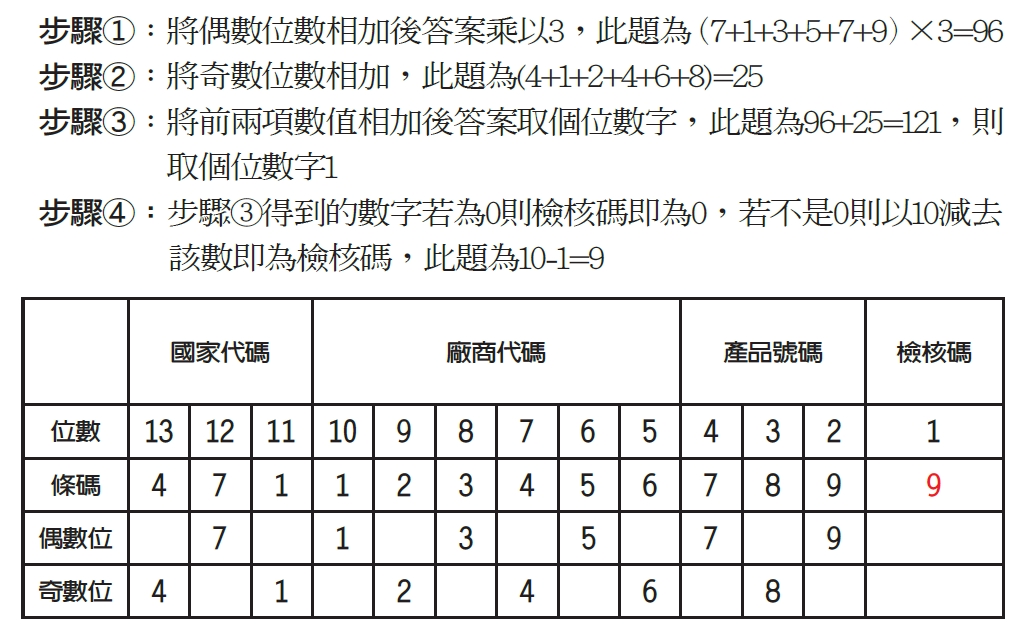
●再看看╱二維條碼怎構成? 兩個一維疊加產生
我們再來說說二維條碼(QR Code)的構成規則,它最初是由2個一維條碼疊加在一起讓X軸、Y軸都帶有訊息而進化成現在有40種尺寸與4種「容錯」級別的二維條碼。QR Code裡每一個黑白方格都是一個位元(bit),黑色方格代表1,白色方格代表0,掃碼時機器只要判斷反光與否,就能將黑白圖像轉換為1與0的組合。其中,最重要的就是位於上方兩側與左下的3個「回」狀定位標記(如圖中標示數字1處),定位標記是讓掃描端能夠辨識QR Code的方向,就像先定義好正向X軸、Y軸和原點後就能判斷出應該從哪裡開始讀取和結束。
為了因應不同大小圖樣的QR Code印刷,因此需要「定位資訊」作為單位刻度,讓掃描器知道最小單位方格大小(如圖中標示數字3處)。根據QR Code發展版本的不同會有不同數量的校正圖塊(如圖中標示數字2處),用以矯正方向與對齊,因此不管使用任何的角度去掃描,或是二維碼不平整,都可以藉由它的定位再加以特殊運算使得QR Code還原到可被解讀。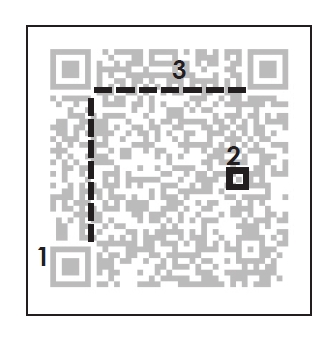
●很厲害╱若有資訊缺失 容錯碼可挽救
了解QR Code的構成後,不得不提其實它最厲害的地方是前面所說的「容錯」,所謂的「容錯」是指當QR Code條碼缺了一角,也就是當部分資訊缺失在容許範圍內,它會拿其他資訊自動填補,讓整體資訊依然可被完整辨識。這樣的容錯碼是如何產生的呢?舉一個例子說明如下:
例如,有一個貨號輸入碼為5247四位數字,我們將此輸入碼設定為m,在產製QR Code時會生成的容錯碼設為p(所以最後的QR Code會是mp),而原本運算程序前就有一組固定碼g。為了方便說明,我們假設一組數字g=12345,現在利用多項式原理:
被除式=除式×商+餘式
將輸入碼m對應為x的7次多項式:
5(x的7次方)+2(的6次方)+4(x的5次方)+7(x的4次方)+0(x的3次方)+0(x的2次方)+0x+0
固定碼g對應為x的4次多項式:
11(x的4次方)4+2(x的3次方)+3(x的2次方)+4x+5
再將m÷g得到的餘式pp即為容錯碼。
●教教你╱位數有負怎麼辦? 「伽羅瓦域」能解決
不過在此會遇到一個問題,就是有可能遇到位數有負的狀況,因此引入一個封閉數域「伽羅瓦域」的運算法:即是在此域中的數值經過有限域的運算, 依然會在此數域中。
我們舉一個在23(即0、1、2、3、4、5、6、7這八個數字)伽羅瓦域的加法、乘法運算(見表一、表二)。這個23「伽羅瓦域」的加法、乘法運算是由這樣的順序得到的: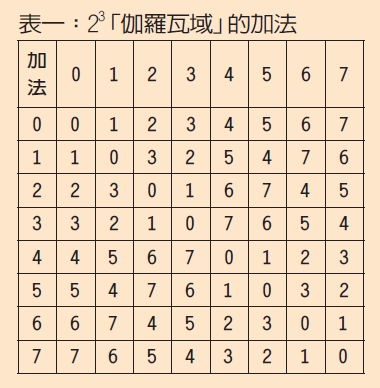
步驟1:將數字轉成「二進制」,例如三位數中:0轉為000、1轉為001、2轉為010、3轉為011、4轉為100、5轉為101、6轉為110、7轉為111。
步驟2-1:如果要做加法或減法(結果相同),只需要藉由「邏輯異或」(簡稱xor,以符號⊕來表示)來完成,xor運算規則是:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如5+6的運算為101⊕110=011,而011即為3(結果還是在伽羅瓦域中)。
步驟2-2:如果要做乘法(除法方式亦同),先將數字轉成二進制後做模二乘法,再以xor運算規則得到答案,答案若超出23值域則需要除以定值1011(稱為本原值)的餘數即為答案。下例就是6×7的運算過程,答案為4。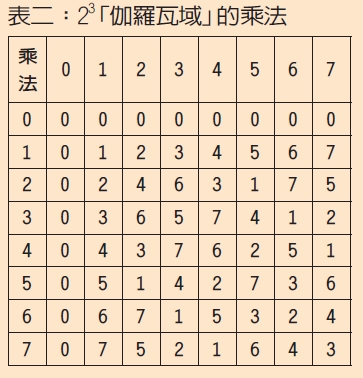
依據上列運算規則,我們可以求m÷g:
因此可得容錯碼p=1421 ,有了這樣的容錯碼,只要驗證mp÷g,若餘數為0,則說明這組QR Code是沒有錯誤的資訊,而一旦餘數不為0則代表資訊有缺,在一定的條件下則可回推原始輸入碼。
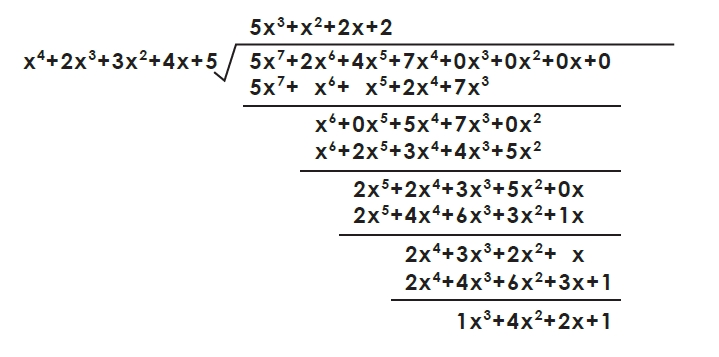
●有妙用╱因為有容錯機制 QR Code更有特色
基於容錯機制,可讓使用者美化QR Code,比方到QR Code製作網站輸入目標網址,再上傳個人頭貼或插圖掩蓋少部分的輸入碼,使其在容錯的機制下依然可讀,如此產生的QR Code更有特色,你也可以試試看!

●作者為教育部高中數學學科中心研究教師、台北市3A教學基地中心主任,獲北市特殊優良教師
原文出自《好讀周報》667期



